How many holes need to be drilled to collapse a wooden cube?

(Phys.org)—It may sound like a simple riddle, but a team of scientists is intrigued with the answer because it could lead to a better understanding of percolation, the process that occurs when a liquid trickles through small holes in a filter. Percolation models have applications in unexpected areas, such as understanding cancer metastasis and in distributed computing.

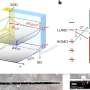
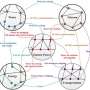
The scenario involves a wooden cube with 6-cm sides made of medium-density fiberboard. Each of the six faces is marked with a 6 x 6-cm square lattice for a total of 36 square cells per face. Then round holes (of diameter equal to the length of a square cell) are drilled through random cells all the way through the cube. Holes continue to be randomly drilled until the structure breaks apart into separate pieces.

Through both experiments and simulations, the researchers found that the number of holes that needs to be drilled to collapse this particular cube is always around 13 holes in each of the three directions, or 39 holes total. Their formula shows that, although this critical number changes for different lattice sizes, the critical density of drills is very similar. (Also, the type of wood doesn't matter, since whatever wood is not drilled is considered intact.) But for the scientists, what's more important than a particular number is how the cube reaches its breaking point.

The researchers, a seven-member collaboration representing institutions in Switzerland, the UK, Brazil, the US, China, Portugal, and Germany, have published a paper on the fragmentation properties due to random drilling in a recent issue of Physical Review Letters.

As the number of drilled holes approaches the critical number, the researchers found that the cube begins to exhibit critical fragmentation properties. Surprisingly, the properties observed here turn out to differ greatly from those observed by researchers 30 years ago using similar models, but before modern simulation technology.

"We find that the statistical properties of drilling are different from the ones of classical percolation—we say in physics of critical phenomena that these two systems fall into different universality classes," coauthor Nuno Araújo, at the University of Lisbon in Portugal, told Phys.org.

Whereas the classical model suggests that random hole-drilling follows random percolation behavior, in the new study the researchers found that the behavior departs from random behavior as the cube approaches its critical breaking point. They found that the cube gradually transitions to this critical point, accompanied by a rich spectrum of critical phenomena. For percolation applications, this finding means that a liquid's transport properties change in a predictable way as the filter it passes through approaches its breaking point.

The results could have diverse applications, including helping researchers better understand how enzymes degrade the gel that surrounds and supports organs and tissues. The structural gel, also called the "extracellular matrix," is often modeled as a cube and the enzyme activity is modeled as random cutting. Understanding enzyme gel degradation is vital for understanding many biochemical processes, including tumor metastasis, since the enzyme "drilling" allows tumor cells to move to other organs.

Percolation models are also used to understand networks, in particular to detect communities within networks. The models apply to many different types of networks, from social networks to distributed computing networks, in which multiple computers communicate with one another to solve problems.

In the future, the researchers plan to investigate how drilling might affect the material's physical properties.

"Percolation is all about connectivity," Araújo said. "In this work we mainly focus on the evolution of the largest connected piece. Other properties that are still unexplored for drilling are the conductivity properties—for example, electric conductivity if the material is a conductor."

© 2016 Phys.org