Scientists develop solutions for the precise simulation of turbulences

Turbulence makes life difficult for the designers of cars or aircrafts. It cannot be simulated with absolute precision. Martin Oberlack, head of Institute of Fluid Dynamics wants an original solution to the problem.

Albert Einstein grins impishly from a poster on the wall in Professor Martin Oberlack's office. Perhaps the genius already knew decades ago that his thinking would lend wings to machine construction engineers like Martin Oberlack and help them to solve apparently unsolvable problems involving aerodynamics. Martin Oberlack explains the problem troubling aircraft and car manufacturers using a diagram hanging on the wall in the corridor of the Institute of Fluid Dynamics on the Darmstadt Lichtwiese.

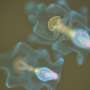
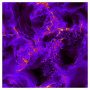
It looks like a brightly coloured abstract painting: a 5-metre long strip with smooth, even brush strokes dominating the left edge that become increasingly chaotic as they approach the right. In fact, it's almost as if the artist became less and less controlled as work progressed. But it's not a work of art. "It's a computer simulation of turbulence," says Professor Oberlack, and displays the vortices of air flowing over a flat panel. The vortices increase towards the right, that is as the gap to the panel increases. "That's why Business Class is at the front of an aircraft," he explains. Vortices at the back of the aircraft make that area noisier, adds the machine construction engineer.

Even supercomputers can not simulate turbulences with absolute precision

Noise isn't the only annoyance caused by turbulence. Vortices also cause air resistance, or drag, which increases fuel consumption. So the shape of a vehicle or aircraft should cause as few air vortices as possible. To establish the best shape, the developers experiment with various different versions in wind tunnels. Computers are also used to help with the design. All this effort, and it's still not quite enough. "Even the most powerful supercomputers in Germany can't simulate turbulence with absolute precision," explains Martin Oberlack. Why not: the less viscous a medium is, the tinier the tiniest vortices are. However, if you want to simulate the occurrence on a computer, it is needed to take vortices of all sizes into account.

Engineers are not interested in every single tiny vortex in the airflow, but in statistical sizes such as the average speed in the air at different distances from the surface, because air resistance can be calculated from this profile. "The tiniest differences in the speed profile matter," he says.

However, the subtle differences in the statistical values can only be derived from a complete simulation of the chaotic event – just as it takes lots of individual opinions in order for the results of a survey to be precise and reliable. This requires computers with vast memories and unimaginable computing speeds. And even though supercomputers are getting ever-faster and their memories ever-bigger, "It's still going to be about 50 years before they can calculate turbulence with a precision that eliminates the need for expensive experiments in wind tunnels," he adds.

In order to reduce computing time, the developers simplify their mathematical models using empirical assumptions that are based on experiments, but that makes the simulations inaccurate. "To an airline, though, the tiniest differences in kerosene consumption matter," he emphasises. And although there is a huge gap between this requirement for exact results and the precision of the simplified simulations, Martin Oberlack doesn't seem to be losing any sleep over it. That's because the gap defines his playing field. He and his 20-strong team are the only people in the world who are ploughing it with a new method. And they have solutions to offer.

So how did that come about? Professor Oberlack has worked closely with physics since the 1990s, at the renowned Stanford University in the USA. A blackboard in his office is covered in formulas known as differential equations. Most of the books in his office are also on this subject. They describe turbulences mathematically, and they are heavy stuff.

And this is where Einstein comes in. "He realized how important symmetries are in physics," says Martin Oberlack. Symmetry exists when rotations, movements or other operations change nothing in the physical description of the system. A merry-go-round, for instance, looks the same on all sides, and in a spruce mono-culture it is not easy to tell whether you are in spot X or 100 metres east of it.

Symmetries make it much easier to solve complex equations. Oberlack's team uses them to simplify the equations used to describe turbulence so that deriving the statistical values is easier and more precise. This enables the team to produce more exact calculations of average speeds.

A hidden kind of symmetry

All well and good. But isn't turbulence the same as chaos – the absence of symmetry? Oberlack considered this question for a long time before carefully replying. It's a hidden kind of symmetry. A comparison illustrates it more clearly. When you pour milk into a cup of coffee, it creates a random, chaotic pattern. However, if you take photos of lots of these patterns and stack them, then the result is an even milky-coffee brown. The statistical observation turns chaos into symmetry.

There is a similar effect in airflow: The speed of the air fluctuates as it travels just over the surface of a body, such as an aircraft fuselage. However, this fluctuation keeps stopping for short periods of time. These breaks in the chaos are called intermittencies, and appear to be random. However, if their occurrence is evaluated statistically, this reveals regularities in their frequency and duration. In the statistics, the values are often distributed evenly around a mean value, such as the size of a body. Although the distribution of the intermittencies isn't quite that symmetrical, more complex symmetries do exist. "They can be used to determine statistical sizes such as air resistance," explains Martin Oberlack.

Now his team wants to integrate his findings in simulation models in order to make the calculations more precise. Based on preparatory work by Dr. Marta Waclawczyk, a former colleague of Martin Oberlack who is now a researcher at the University of Warsaw, the doctoral candidate Andreas Zieleniewicz is working on them. However, Oberlack has little hope that the optimum designs for vehicle chassis or aircraft fuselages will be spilling forth from the computer any time soon. "So far, our method has only worked on basic systems," he says, including tunnel or pipe flows.

However, the machine constructor with a passion for physics is quick to emphasise that this is all basic research. But the team of scientists is researching further symmetries in the apparent chaos that could make their method more powerful, and therefore of interest for complex industrial applications. Although these symmetries do exist, they are too complex to be fully understood, explains Oberlack. "We have the justified hope that we will come to understand them." The Darmstadt researchers' unfaltering curiosity could soon be used on aircraft.