January 29, 2016 feature
Earthquake power laws emerge in bamboo chopsticks (w/ video)
(Phys.org)—Whereas a dry twig can be broken with a single snap, breaking a bamboo chopstick produces more than 400 crackling sounds. In a new study, researchers have found similarities between the complex acoustic emission of breaking a bamboo chopstick and the three famous power laws that describe earthquake activity. The scientists also propose that the underlying mechanism behind these laws may be simpler than currently thought.
The researchers, Sun-Ting Tsai et al., from National Tsing Hua University, have published their paper on the sounds of breaking a single bamboo chopstick in a recent issue of Physical Review Letters.
Bamboo and earthquakes
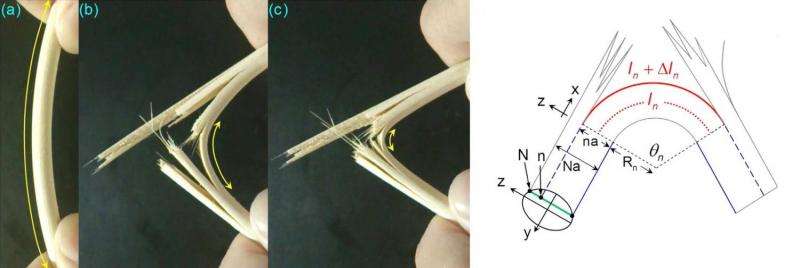
Bamboo is made of a bundle of fibers, similar to how a handful of uncooked spaghetti is made of a bundle of noodles. When a chopstick breaks, each fiber cracks at a different time. Further, a single fiber within a bundle breaks only a little bit at a time. This produces a multitude of crackling sounds: about 80 main cracks (roughly corresponding to the number of fibers) and four to eight smaller cracks following each main crack, in analogy with an earthquake's main shock and many smaller aftershocks.
Like many natural phenomena, the breaking of a bamboo chopstick does not happen randomly. The researchers showed that the crackling sounds mimic earthquake activity by closely following the three main seismic power laws.
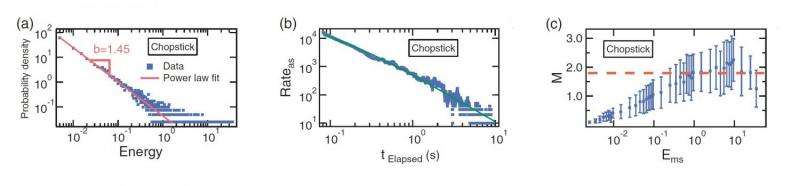
First, the researchers found that quieter (lower-energy) sounds are much more common than louder (higher-energy) sounds, and the distribution of sounds in terms of their acoustic energy follows a power law similar to the Gutenberg-Richter law. This law describes how much more common smaller-magnitude earthquakes are than larger-magnitude earthquakes.
Second, the rate of bamboo aftershocks decreases quickly after the main shock. This rate is described by a power law that is very similar to Omori's law, which shows that the likelihood that an aftershock will occur decreases more and more each day after the initial quake, also in a power-law fashion.
Third, in the bamboo chopstick, the ratio between the magnitude of the main shock and that of the largest aftershock does not depend on the magnitude of the main shock. This observation follows Båth's law, which says the same thing for earthquakes.
This is not the first time that the acoustic emission of a fractured material has been compared to an earthquake. Previous research has found similarities in the sounds of breaking wooden plates, paper, rock, concrete, and even charcoal.
"The fact that similar research has been around and popular for a long time implies that people believe that there are profound secrets hidden behind these empirical laws, and a lot can be learned by making the analogy to earthquakes," coauthor Tzay-Ming Hong, a physics professor at National Tsing Hua University, told Phys.org.
Hidden simplicity in the laws
In the previous acoustic emission studies, only the experimental findings were reported, and no theory was proposed to explain the findings. This is partly because the mechanism behind these power laws has appeared to be complicated. Typically, the power laws for earthquakes are derived using concepts that describe dynamical systems, such as phase transitions, self-organized criticality, and fractals.
Here, however, the researchers have shown that all three laws can be derived in a simpler way, from a geometric model of a bamboo chopstick.
"You may ask, how could we be so daring as to complement our experiments with a theoretical model that deviates from the mainstream approach?" Hong said. "The reason is that the chopstick (or the bundle of spaghetti) is so simple and clean. I believe that, after realizing that these systems exhibit all three major seismic laws, most people will be inclined to search for an easier explanation."
The simple model may also help explain why certain patterns seem to keep reemerging in diverse and surprising places.
"The simplicity of a bamboo chopstick prompts us to suspect that these laws may be more common than people thought or are willing to accept," Hong said.
The downside to the simplicity, however, is that unravelling the secret to these laws may not offer much help in improving earthquake prediction.
"Whether our analogy and model can be of any use to the fracture dynamics or seismology in general is for others to judge," Hong said.
However, the results could still be useful in another way. They could help explain why sound intensity can be compared to the magnitude of a tremor—or a "shake," as Hong puts it—in the first place.
"One contribution from our paper that is not as splashy as the Gutenberg-Richter law may indeed have some immediate practical use," he said. "Previous acoustic studies were content at reporting just the analogy with earthquakes, but never really explained why the intensity of sound should be compared to the amount of shake energy. You may think that sound comes from shake. But you forget that it is not true the other way around. That is, not all shakes produce sounds. There is no one-to-one correspondence between these two events. Therefore, establishing their correlation is crucial for future applications that use the detection of sound to monitor and determine possible fractures of, say, bridges, building, or machines that are hidden from plain view."
More information: Sun-Ting Tsai, et al. "Acoustic Emission from Breaking a Bamboo Chopstick." Physical Review Letters. DOI: 10.1103/PhysRevLett.116.035501 . Also at arXiv:1509.00631 [cond-mat.soft]
Journal information: Physical Review Letters
© 2016 Phys.org