May 1, 2015 feature
Occam's razor redux: A simple mathematical approach to designing mechanical invisibility cloaks
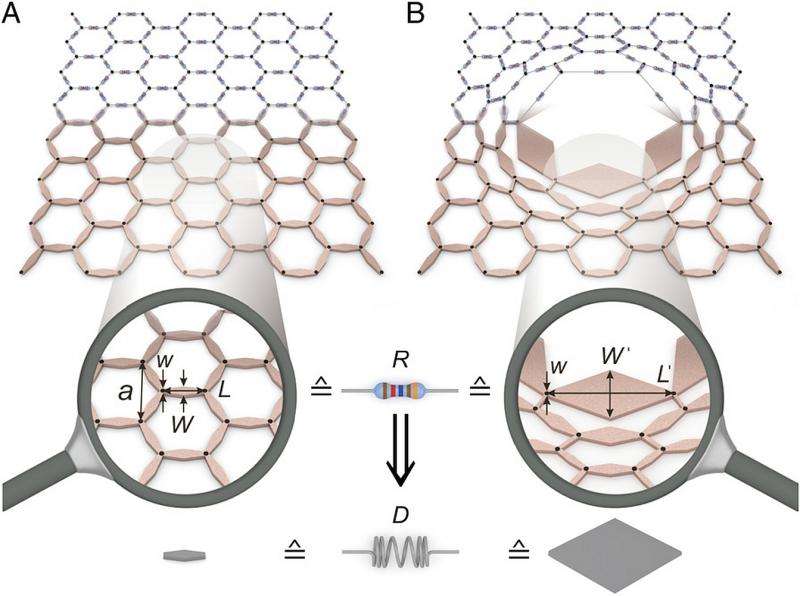
Metamaterials – engineered materials with properties not found in nature – have led to an astounding range of optical, acoustic, thermodynamic, two-dimensional solid mechanics, and other types of invisibility cloaks that render the cloaked object indistinguishable from the environment around them – but the ability to cloak three-dimensional solid mechanics has proven elusive. (Solid mechanics is the branch of continuum mechanics – which models materials as a continuous mass rather than as discrete particles – that studies the behavior of solid materials, especially their motion and deformation under the action of forces, temperature changes, phase changes, and other external or internal agents.) Recently, however, scientists at Karlsruhe Institute of Technology, Germany – following their design last year of a so-called unfeelability cloak1 that hides (at this point small) 3D objects such that they cannot be physically detected – have demonstrated a surprisingly simple and generalizable approach in which a coordinate transformation – a mathematical process of obtaining a modified set of coordinates by performing some nonsingular operation on the coordinate axes, such as rotating or translating them – is mapped directly onto a concrete one-component microstructure. In addition, the researchers have successfully applied the technique to static elastic–solid mechanics (the elastic and plastic behavior of solid objects subject to stresses and strains) to a material made of printed polymer.
Researcher Tiemo Bückmann discussed the paper he and his colleagues published in Proceedings of the National Academy of Sciences, as well as the challenges they faced in developing their concept and conducting the resulting research. "The main challenge in devising our approach – that is, of directly transforming the lattice points of a 2D discrete lattice composed of a single constituent material while keeping the properties of the elements connecting the lattice unchanged – was actually to come up the concept and think about realizing it," Bückmann tells Phys.org. "At first, we just used that concept as an example to illustrate the basic concepts of cloaking, since it was taking us quite some time to really think about realizing such a structure out of one material – but this then worked so nicely that it was surprising even to us."
Another issue: cloaking a void in an effective elastic material with respect to static uniaxial compression as an example of elastic–solid mechanics. "Our main problem here was, first of all, that the mathematical background for a material parameter transformation is extremely complex," Bückmann notes. "This makes the design of such a cloak highly complex as well as extremely demanding on materials and their effective properties." That said, the scientists found that these problems were all solved by their straightforward approach of simply transforming the lattice points rather than effective material properties. "This simplified the cloaking concept enormously, making it possible for us to create a cloak along these lines."

A third obstacle was comparing the average relative standard deviation of the strain vectors outside of the cloaked void with respect to the homogeneous reference lattice as a way of quantifying cloaking quality. "We thought about a way of quantifying the performance of our cloak, and so searched for a good quantity that is actually sensitive and, at the same time, representative for the performance of a cloak. We came up with the differences as a standard deviation between two samples."
Bückmann tells Phys.org that two insights were key to addressing these challenges. "First of all, we found the general concept of a lattice transformation cloak, which is applicable to many different physical quantities. Furthermore, we discovered that the concept also works in mechanics – one of the most demanding fields of physics with regard to cloaking." This general concept is easy to understand, he points out, and therefore will hopefully help design a range of structures and solve problems in mechanical and engineering science.

An interesting limitation to the new approach – which is applied to the cloaking of a void in a lattice material – is that cloaking will never be perfect. "This is rather a general statement, as one needs to keep in mind that a perfect cloak is directly linked to material parameters that diverge," Bückmann tells Phys.org. "This means if one would like to cloak an object, infinite materials parameters occur, such as an infinite mass at the inner cloaking radius – and this cannot be fulfilled in an actual experiment. One needs thus to consider how well an actual cloak performs, that is, Am I able to detect the imperfections, or do I care at all about them? This in turn depends on the problem one needs to solve, and cannot be answered in general." In short, mathematically perfect cloaking is unavoidably connected with singular material parameters that just cannot be achieved in reality.
In showing that the approach works in various areas, the researchers evaluated the main concepts of cloaking based on a lattice material, considering only static measurements. "Within these fields, Bückmann notes, "one can cloak in general any kind of physical problem that is linked to the same equations. A few examples in addition to mechanics, as presented in our paper," he illustrates, "are current conduction, heat conduction, electrostatic potential, magnetostatics, and diffusion." To underscore the effectiveness of their approach, Bückmann points out that while there were slight differences in the areas tested, in general – depending on the transformation and the given loading conditions – all simulations performed showed a relevant improvement over the case prior to our applying our transformation. "As one tries to cloak a larger and larger hole, or void, in a very thin cloaking shell," he explains, "the performance of course decreases."

In addition to performing dynamic studies on the cloaks described in the paper, the scientists are now searching for new ways to cloak, as well as a method for introducing the cloaking concept into additional dimensions. "Our approach can help design strong materials in complex shapes without losing the performance of the initial material. We hope to use this approach in the engineering sciences to find a way to design complex architectures in a lightweight fashion – specifically in civil engineering and the automotive industry, where low weight and strong lattice-based materials will be, and in fact already are, a key future technology. For example," Bückmann illustrates, "think about a door in a carbon-enforced car. Here one would directly find the right fiber directions to enforce the opening in the car without losing the car's overall stiffness."
More information: Mechanical cloak design by direct lattice transformation, Proceedings of the National Academy of Sciences (2015) 112(16):4930-4934, doi:10.1073/pnas.1501240112
Related:
1An elasto-mechanical unfeelability cloak made of pentamode metamaterials, Nature Communications (2014) 5:4130, doi:10.1038/ncomms5130
Journal information: Proceedings of the National Academy of Sciences , Nature Communications
© 2015 Phys.org