Algorithm reduces size of data sets while preserving their mathematical properties

As anyone who's ever used a spreadsheet can attest, it's often convenient to organize data into tables. But in the age of big data, those tables can be enormous, with millions or even hundreds of millions of rows.
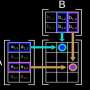
One way to make big-data analysis computationally practical is to reduce the size of data tables—or matrices, to use the mathematical term—by leaving out a bunch of rows. The trick is that the remaining rows have to be in some sense representative of the ones that were omitted, in order for computations performed on them to yield approximately the right results.
At the ACM Symposium on Theory of Computing in June, MIT researchers will present a new algorithm that finds the smallest possible approximation of the original matrix that guarantees reliable computations. For a class of problems important in engineering and machine learning, this is a significant improvement over previous techniques. And for all classes of problems, the algorithm finds the approximation as quickly as possible.
In order to determine how well a given row of the condensed matrix represents a row of the original matrix, the algorithm needs to measure the "distance" between them. But there are different ways to define "distance."
One common way is so-called "Euclidean distance." In Euclidean distance, the differences between the entries at corresponding positions in the two rows are squared and added together, and the distance between rows is the square root of the resulting sum. The intuition is that of the Pythagorean theorem: The square root of the sum of the squares of the lengths of a right triangle's legs gives the length of the hypotenuse.
Another measure of distance is less common but particularly useful in solving machine-learning and other optimization problems. It's called "Manhattan distance," and it's simply the sum of the absolute differences between the corresponding entries in the two rows.
Inside the norm
In fact, both Manhattan distance and Euclidean distance are instances of what statisticians call "norms." The Manhattan distance, or 1-norm, is the first root of the sum of differences raised to the first power, and the Euclidean distance, or 2-norm, is the square root of the sum of differences raised to the second power. The 3-norm is the cube root of the sum of differences raised to the third power, and so on to infinity.
In their paper, the MIT researchers—Richard Peng, a postdoc in applied mathematics, and Michael Cohen, a graduate student in electrical engineering and computer science—demonstrate that their algorithm is optimal for condensing matrices under any norm. But according to Peng, "The one we really cared about was the 1-norm."
In matrix condensation—under any norm—the first step is to assign each row of the original matrix a "weight." A row's weight represents the number of other rows that it's similar to, and it determines the likelihood that the row will be included in the condensed matrix. If it is, its values will be multiplied according to its weight. So, for instance, if 10 rows are good stand-ins for each other, but not for any other rows of the matrix, each will have a 10 percent chance of getting into the condensed matrix. If one of them does, its entries will all be multiplied by 10, so that it will reflect the contribution of the other nine rows it's standing in for.
Although Manhattan distance is in some sense simpler than Euclidean distance, it makes calculating rows' weights more difficult. Previously, the best algorithm for condensing matrices under the 1-norm would yield a matrix whose number of rows was proportional to the number of columns of the original matrix raised to the power of 2.5. The best algorithm for condensing matrices under the 2-norm, however, would yield a matrix whose number of rows was proportional to the number of columns of the original matrix times its own logarithm.
That means that if the matrix had 100 columns, under the 1-norm, the best possible condensation, before Peng and Cohen's work, was a matrix with hundreds of thousands of rows. Under the 2-norm, it was a matrix with a couple of hundred rows. That discrepancy grows as the number of columns increases.
Taming recursion
Peng and Cohen's algorithm condenses matrices under the 1-norm as well as it does under the 2-norm; under the 2-norm, it condenses matrices as well as its predecessors do. That's because, for the 2-norm, it simply uses the best existing algorithm. For the 1-norm, it uses the same algorithm, but it uses it five or six times.
The paper's real contribution is to mathematically prove that the 2-norm algorithm will yield reliable results under the 1-norm. As Peng explains, an equation for calculating 1-norm weights has been known for some time. But "the funny thing with that definition is that it's recursive," he says. "So the correct set of weights appears on both the left-hand side and the right-hand side." That is, the weight for a given matrix row—call it w—is set equal to a mathematical expression that itself includes w.
"This definition was known to exist, but people in stats didn't know what to do with it," Peng says. "They look at it and think, 'How do I ever compute anything with this?'"
What Peng and Cohen prove is that if you start by setting the w on the right side of the equation equal to 1, then evaluate the expression and plug the answer back into the right-hand w, then do the same thing again, and again, you'll quickly converge on a good approximation of the correct value of w.
"It's highly elegant mathematics, and it gives a significant advance over previous results," says Richard Karp, a professor of computer science at the University of California at Berkeley and a winner of the National Medal of Science and of the Turing Award, the highest honor in computer science. "It boils the original problem down to a very simple-to-understand one. I admire the mathematical development that went into it."
More information: "ℓp Row Sampling by Lewis Weights." arxiv.org/abs/1412.0588
Provided by Massachusetts Institute of Technology
This story is republished courtesy of MIT News (web.mit.edu/newsoffice/), a popular site that covers news about MIT research, innovation and teaching.