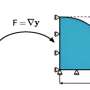
Yes, black holes exist in gravitational theories with unbounded speeds of propagation
Lorentz invariance (LI) is a cornerstone of modern physics, and strongly supported by observations.
In fact, all the experiments carried out so far are consistent with it, and no evidence to show that such a symmetry needs to be broken at a certain energy scale. Nevertheless, there are various reasons to construct gravitational theories with broken LI. In particular, our understanding of space-times at Plank scale is still highly limited, and the renomalizability and unitarity of gravity often lead to the violation of LI.
One concrete example is the Horava theory of quantum gravity, in which the LI is broken in the ultraviolet (UV), and the theory can include higher-dimensional spatial derivative operators, so that the UV behavior is dramatically improved and can be made (power-counting) renormalizable.
On the other hand, the exclusion of high-dimensional time derivative operators prevents the ghost instability, whereby the unitarity of the theory—a problem that has been faced since 1977 [ K.S. Stelle, Phys. Rev. D 16, 953 (1977)]—is assured. In the infrared (IR) the lower dimensional operators take over, whereby a healthy low-energy limit is presumably resulted.
However, once LI is broken different species of particles can travel with different velocities, and in certain theories , such as the Horava theory mentioned above, they can be even arbitrarily large. This suggests that black holes may not exist at all in such theories, as any signal initially trapped inside a horizon can penetrate it and propagate to infinity, as long as the signal has sufficiently large velocity (or energy). This seems in a sharp conflict with current observations, which strongly suggest that black holes exist in our universe [R. Narayan and J.E. MacClintock, Mon. Not. R. Astron. Soc., 419, L69 (2012)].
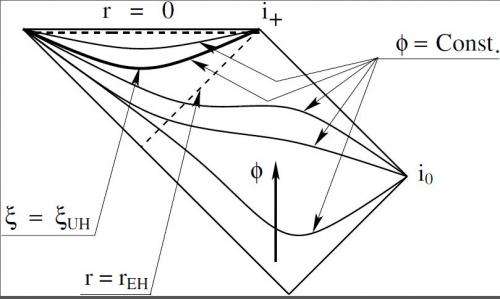
A potential breakthrough was made recently by Blas and Sibiryakov [D. Blas and S. Sibiryakov, Phys. Rev. D84, 124043 (2011)], who found that there still exist absolute causal boundaries, the so-called universal horizons, and particles even with infinitely large velocities would just move around on these boundaries and cannot escape to infinity.
This has immediately attracted lot of attention. In particular, it was shown that the universal horizon radiates like a blackbody at a fixed temperature, and obeys the first law of black hole mechanics [P. Berglund, J. Bhattacharyya, and D. Mattingly, Phys. Rev. D85, 124019 (2012); Phys. Rev. Lett. 110, 071301 (2013)]. The main idea is as follows: In a given space-time, a globally timelike foliation parametrized by a scalar field, the so-called khronon, might exist.
Then, there is a surface at which the khronon diverges, while physically nothing singular happens there, including the metric and the space-time. Given that the khronon defines an absolute time, any object crossing this surface from the interior would necessarily also move back in absolute time, which is something forbidden by the definition of the causality of the theory. Thus, even particles with superluminal velocities cannot penetrate this surface, once they are trapped inside it.
In all studies of universal horizons carried out so far the khronon is part of the gravitational theory involved. To generalize the conception of the universal horizons to any gravitational theory with broken LI, recently Lin, Abdalla, Cai and Wang promoted the khronon to a test field, a similar role played by a Killing vector, so its existence does not affect the given space-time, but defines the properties of it.
By this way, such a field is no longer part of the underlaid gravitational theory and it may or may not exist in a given space-time, depending on the properties of the space-time considered. Then, they showed that the universal horizons indeed exist, by constructing concrete static charged solutions of the Horava gravity. More important, they showed that such horizons exist not only in the IR limit of the theory, as has been considered so far in the literature, but also in the full Horava theory of gravity, that is, when high-order operators are not negligible.
More information: The corresponding author of this paper is Anzhong Wang, anzhong_wang@baylor.edu, and the paper can be found in the International Journal of Modern Physics D, via the following link, www.worldscientific.com/doi/ab … 42/S0218271814430044 . Access the PDF directly from www.worldscientific.com/doi/pd … 42/S0218271814430044 .
Journal information: Physical Review Letters
Provided by World Scientific Publishing