November 3, 2014 feature
Mathematicians settle 30-year-old resonance controversy
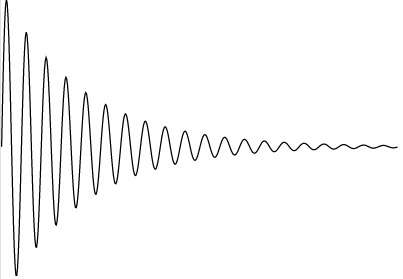
In the early '80s, several researchers were working to determine the location of atomic and molecular resonances, which are the frequencies at which atoms and molecules prefer to oscillate. Two groups of researchers (Rittby, et al., and Korsch, et al.), each using a different method, came up with different locations for these resonances. Settling the dispute proved to be extremely difficult due to the fact that neither method could predict the actual resonances, but instead simply gave approximations. In fact, at the time there was no way to locate resonances with absolute certainty.
The controversy remained unsettled for the last 30 years. But now in a new study, mathematicians have presented a method that, for the first time, can locate resonances with absolute certainty and high accuracy. The method can also tell when approximations fail to lie near true resonances. Using this method, the researchers could show which approximations from the two groups in the '80s were accurate, and which were not, finally settling the controversy.
The mathematicians, Sabine Bögli, et al., from the University of Bern in Switzerland, Cardiff University in the UK, Stockholm University in Sweden, and Regensburg, Germany, have published their paper on the new method for determining resonances in a recent issue of the Proceedings of The Royal Society A.
A key ingredient in the new method is interval arithmetic. By operating on intervals rather than numbers, interval arithmetic allows every computational step to be carried out with absolute certainty. Interestingly, interval arithmetic has recently been used in a variety of areas, including navigation of an autonomous robotic sailboat, optimization of a spacecraft traveling between planets, and improvement of stability in particle accelerators.
In this study, the researchers used interval arithmetic to prove with absolute certainty that the approximations of resonances in Rittby, et al., do lie near true resonances, whereas the approximations of higher resonances in Korsch, et al., do not.
The new method also reveals additional information, in particular the existence of two new pairs of resonances that were originally suggested in a previous paper (Abramov, et al.), but not predicted by either Rittby, et al., or Korsch, et al. The researchers explained that this part was the most challenging because these pairs are so close to the imaginary axis, and the resonances in each pair are so close to each other. The results could have implications for a wide variety of areas.
"Resonances are ubiquitous in physics, e.g., in mechanics, acoustics, and electrical circuits," coauthor Marco Marletta, Professor at Cardiff University in the UK, told Phys.org. "In atomic physics, resonances are associated with metastable states of a system having a sufficiently long lifetime to be well-characterized and to render them significant experimentally and theoretically. The imaginary part of a resonance is related to the decay rate or inverse lifetime of the system."
The researchers explained that the work could be applied to some very computationally challenging problems.
"For problems with complex eigenvalues (such as resonances in complex scaling), numerical computations are prone to be unreliable because small errors in input data may result in large errors in the results and/or because spurious eigenvalues may occur (spectral pollution)," explained coauthor Christiane Tretter, Professor at the University of Bern in Switzerland, and from Stockholm University in Sweden. "Therefore methods guaranteeing absolute certainty such as interval arithmetic may prove to be highly useful."
More information: Sabine Bögli, et al. "Guaranteed resonance enclosures and exclosures for atoms and molecules." Proceedings of The Royal Society A. DOI: 10.1098/rspa.2014.0488
Journal information: Proceedings of the Royal Society A
© 2014 Phys.org