Mapping the relationship between two quantum effects known as topological insulators
At very low temperatures and under strong magnetic fields, thin films of semiconducting materials can display a phenomenon known as the quantum Hall (QH) effect, which can allow electrons to flow with no energy loss. In a newly discovered class of materials known as topological insulators, the same state can be achieved without an external magnetic field, spurring interest in the development of low-power electronics and other promising applications.
Researchers from the RIKEN Center for Emergent Matter Science, the University of Tokyo and Tohoku University in Japan have now experimentally mapped the relationship between the quantum anomalous Hall (QAH) effect in topological insulators and the well-known QH effect in semiconductors, which should facilitate the development of QAH-based technologies.
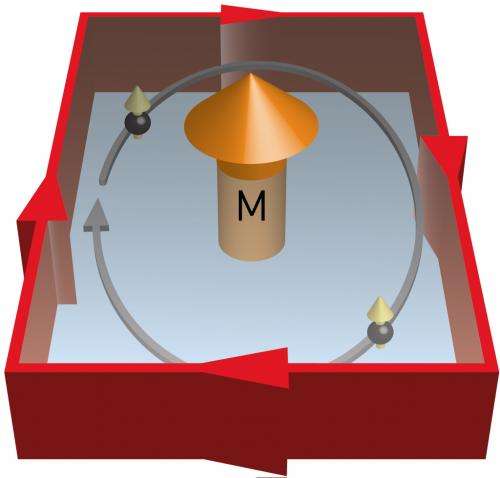
Topological insulators are electrically insulating in their bulk but metallically conductive at their surfaces. The QAH state occurs in these materials at low temperatures when ferromagnetic forces around magnetic ions interact with conductive surface electrons (Fig. 1).
The researchers conducted experiments to investigate whether the same rules that govern the formation of conventional QH states also apply to the QAH effect. They fabricated a topological insulator, chromium-doped bismuth antimony telluride, and placed it in a special circuit that allows the conductivity to be measured in two dimensions while varying the sample temperature or charge carrier density.
As the charge carrier density of the sample was varied and the conduction state moved to the QAH state, the researchers saw that the electron conductivities maintained similar characteristics and an identical, quantized minimum conductance value. Temperature-dependent measurements of the QAH system also revealed a crossover from an insulating to a metallic state—a transformation that also occurs in QH states.
According to Ryutaro Yoshimi from the research team, this is clear evidence that the quantization rules for both quantum Hall effects are the same and that they can be understood within the framework of the same quantized phenomenon. "This is quite a surprising finding because the origins of the QAH and QH effects are completely different," he notes.
The team then plotted the conductivity data onto a two-dimensional map to determine the stable and unstable points of electron state flow in the quantized system. "The map gives us a way to immediately visualize if a material shows the QAH effect when cooled," says Yoshimi. "When we consider the universality of quantum conductivity in various materials, this map becomes quite useful."
More information: Checkelsky, J. G., Yoshimi, R., Tsukazaki, A., Takahashi, K. S., Kozuka, Y., Falson, J., Kawasaki, M. & Tokura, Y. "Trajectory of the anomalous Hall effect towards the quantized state in a ferromagnetic topological insulator." Nature Physics 10, 731–736 (2014). DOI: 10.1038/nphys3053
Journal information: Nature Physics
Provided by RIKEN