Scientists predict coreless vortex in ultracold atoms
Swirling, persistent vortices can be created in superfluid helium. Generally no atoms sit at the eye of these miniature hurricanes. Things might be different in condensates of ultracold atoms. Theorists at the Joint Quantum Institute predict that for some elements a vortex of atoms can be produced which pivots around another sample of atoms at rest in the middle. Such a quantum gimbal has been observed in condensates of two atomic species but never before in a swarm of exclusively one type of atoms in a state of lowest energy.
The JQI search for new forms of quantum reality occurs not in an actual lab. Instead it takes place in a dedicated computer which, over hundreds of hours, simulates the magnetic interactions of a million atoms or so under various conditions. When the "experiment" is over the researchers take the numerical results and plot them up as if they were maps showing the disposition of actual atoms—-either their positions in space or the directions of their spins (as if the atoms were little bar magnets).
In effect the simulation probes atomic matter for new types of magnetic order. It deduces what happens when magnetic atoms, such as those of the element dysprosium, are cooled into a Bose Einstein condensate (BEC) and then subjected to laser beams that make the atoms' interactions spin-dependent. The strength of the interaction is also proportional to the density of atoms; squeeze more and more atoms into the ensemble and a variety of patterns—-so called "spin textures"—-emerges in succession. The results, published in the journal Physical Review Letters (see first related publication), reveals the occurrence of coreless vortices and shows an array of five such new magnetic phases, a feat interesting enough for the JQI paper to have received an "editor's pick" designation in the journal.
SPINOR CONDENSATES
Why use dysprosium? Because it is (along with holmium) the most magnetic of the elements. Indeed, its magnetic dipole moment is ten times stronger than that for rubidium, an element used in many Bose Einstein condensate (BEC) experiments. This makes Dy a potential workhorse for experiments attempting to find new states of magnetic matter. Dy has a complement of 66 electrons which can arrange themselves into seventeen different lowest-energy (groundstate) configurations. So when Dy is chilled low enough in temperature you get not one but seventeen different BECs, all pretty much residing on top of each other in the center of an atom trap. Another name for a BEC consisting of co-existing, multiple-spin orientations is "Spinor condensate."
SPIN-ORBIT COUPLING
This co-existence can be made more complicated in an interesting way by exposing the atoms to a pair of laser beams. This has the effect of toggling the atoms—-which lie mostly in a plane—-from one internal energy level to another. The effectiveness of this toggling is proportional to the velocity of the atoms. Thus an internal state of each atom (the energy levels) is coordinated with an external state of the atom, namely its velocity. This coordination is referred to as spin-orbit coupling, an expression that dates back to the early days of quantum physics, when scientists studied the important force between an electron's spin and the magnetic field created by the fact that the electron was orbiting within the atom. In this early work, spin-orbit coupling could be viewed as a form of self-interaction.
More recently spin-orbit coupling was demonstrated for the first time (see related articles) in a JQI experiment with ultracold rubidium atoms; here the "orbit" in spin-orbit coupling refers not to the motion of electrons within an atom but the motion of the atoms themselves.
MAGNETIC PHASES
The effect of turning on those lasers is to "dress" the atoms. After the laser light is applied the energy levels of the atoms are so prominently reconfigured that only two of the original 17 ground states are still effectively retained in the atom trap for detailed study. These two remaining spin species—-called for convenience spin-up and spin-down—-form an ideal way of exploring strong interactions in a gas of ultracold atoms, all participating in a single gigantic quantum state which allows the atoms to be oriented in two ways—-with their spins up or down.
In conventional matter, magnetism appears in many forms. Some of the more important are ferromagnetic ordering, in which domains (small volumes within the material) aligned together by an external magnetic field remain aligned even after the field is turned off. In anti-ferromagnets, the domains alternate in an aligned-antialigned checkerboard pattern (that is, neighboring domains are oppositely aligned). In paramagnetism regions (atoms or domains) will be attracted or aligned with an external applied field but will lose the alignment when the field is turned off.
In conventional materials, the types of magnetism depend on the intrinsic nature of the material and on impurities present. In ultracold atoms, by contrast, there are no impurities and the magnetism can be engineered at will by adjusting the laser beams (the light used to "dress" the atoms) and the density of the atoms. In a JQI experiment conducted several years ago laser beams were first used to create spin-dependent forces in cold atoms. The researchers, led by Ian Spielman, noticed something else: the atoms with different spin segregated themselves in space (see related articles).
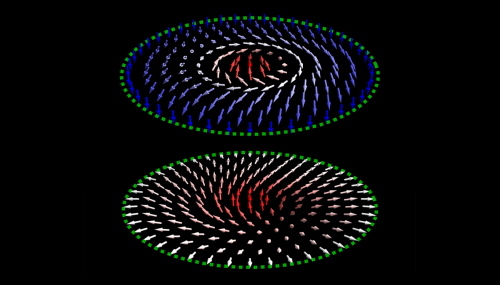
With ultracold Dy atoms, new magnetic phases are expected to appear when the strength of the inter-atomic force is turned up by adding more atoms, and this is what the present JQI work addresses. Here too an expected self- segregation of atoms takes place. In the diagrams below, the two ground-state conditions (spin up and spin down) are depicted as red and blue. And like oil and vinegar separating themselves in an unshaken bottle of salad dressing, the red and blue occupy separate regions of space.
TOPLOGICAL ORDER
Two of the newly found magnetic phases merit particular attention since they possess topological order. In atomic research "topological" has come to refer to a system or a material whose properties don't change even when subjected to perturbations such as the appearance of defects in the layout of the material or if the geometry of the material is distorted in various ways. (When a coffee cup is pulled into the shape of a donut, the geometry certainly changes, but the topology—-how many holes does the object have?—-stays the same.) When this topological invariance is manifested in the persistence of a quantum state or the flow of an electrical current or the propagation of light through a fiber without dissipation, topological immunity from perturbations is a potentially valuable attribute (solid material, photonic circuit, or swarm of ultracold atoms) for a material being considered as a platform for storing or processing information in a future quantum computer (see related articles).
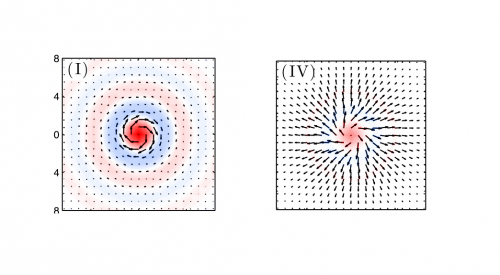
Two of the notable magnetic textures observed in the JQI simulations are called the Skyrmion phase (the name arising originally from particle physics research conducted by Tony Skyrme) and the Meron phase (Greek for fractional). These phases will be described in more detail below. In the meantime, you can observe the spin texture for these phases in the following pictures, which map the average spin value of the condensate of Dy atoms across the two-dimensional plane in which the atoms lie. The deepness of the color (red for up and blue for down) shows how many atoms are pointing up or down respectively, while the length of the black arrows show the strength of the spin at that point in the plane.
CORELESS VORTEX
One can see that the two species of dysprosium atoms (remember that the condensate consists of co-existing sub-populations with spins pointing up or down) are segregated. What this graph doesn't show is that the center population of atoms are mostly at rest, while a band of outlying blue atoms circulates in cyclone fashion.
Where does the circulation come from? One of the authors of the JQI study, Brandon Anderson, explains as follows: "The spin-orbit coupling is what sets the atoms in motion. The atoms can have two types of angular momentum: spin or orbital (around the center of the trap). What SOC does in this case is exchange one unit of spin angular momentum for one unit of orbital angular momentum."
The Skyrmion phase occurs when the density of atoms in the trap is relatively small, about 10^11 atoms per cubic centimeter and the magnetic interactions are relatively weak. In further simulations the density is increased, and the researchers expected that the contending magnetic forces would result in a rather uniform ferromagnetic-like pattern of aligned spins, and this is indeed what happens.
But when they increased the atom density up to a value of 1014—-at which point the magnetic forces were a thousand-fold stronger than for the Skyrmion phase—-a big surprise happened. Things got interesting again.
"This new magnetic phase was totally unexpected," said Ryan Wilson, the lead author on the JQI paper. "The Skyrmion state had been predicted before, but we are the first to demonstrate that a 'Meron' spin texture could appear for atoms in their lowest-energy ground state. This is an emergent, collective-behavior phenomenon: you wouldn't have guessed this structure would have appeared from knowledge of single atom-atom interactions." In the Meron state the spins point away from the center of the trap.

INVERSE MERCATOR
The Skyrmion and Meron states have a superficial similarity: they both feature a "coreless vortex" in which a motionless blob of spin-up atoms is surrounded by a circulating band of spin-down atoms. The difference between the Skyrmion and Meron states comes out more clearly when these planar spin maps are transposed onto a sphere—-a sort of reversal of the process by which a Mercator projection takes points from around the surface of a globe and plots them on a planar map which can spread out on a table. For Gerardus Mercator (1512-1594) the purpose was to provide practical navigation routes for explorers. The purpose for the mapping patterns of magnetic behavior onto a sphere is to exhibit the inherent topology of the system by showing what happens to the spin value of the condensate far from the center.
Let's stop to consider that what these maps show. The condensate of atoms is, first of all, a gigantic quantum in a superposition of spin states. It is a qubit spread out, as it were, across a million atoms, each of which can be in a mixture of orientations, spin-up and spin-down. What we call a spin map is really a map of the wavefunction for the condensate at places point-by-point across the face of the plane. The wavefunction for a quantum object is itself a map for the likelihood that the object will possess certain values—-in this case the average spin of the condensate—-at all those points in space.
In these diagrams the arrow at the North Pole represents the spin of the condensate at the very center of the sample. The several other arrows on this sphere (the one on the left) proceeding down in latitude along any one longitude correspond to the spin as you proceed out radially on the planar map. The South Pole corresponds to the spin of the condensate at the far horizon of the plane—-think of it as infinity. Even though the number of atoms (and the net spin of the condensate) would be very small out there it still worth knowing what the spin orientation would be.
Now look at the diagram for the Meron phase. Marching downwards in latitude over the sphere along a single longitude we come to the bottom (infinitely out in the plane) and things are very different. The spin has reclined so that it sticks out not perpendicularly but at a tangent. But if we make such a sequence of arrows for all the longitudes, the arrows, as we approached the South Pole, would all be pointing in different directions, very much different from the Skyrmion state where the spins all point downwards.
The conundrum of all the spins pointing in different directions for the Meron is nothing less than a mathematical singularity. In the Skyrmion state, if we were to climb back up in latitude, the spin arrow comes all the way around to where it started; we say that the Skyrmion state's "topological charge," or its winding number, has a value of one. For the Meron state, the arrow—-even if it could negotiate the weirdness at the South Pole—-would only come half way back to where it started at the North Pole. The Meron's topological charge is one-half.
Meron states have been predicted to exist in spinor condensates but only for atoms in an excited state, not (as here) for atoms in a ground state. This state is also rather striking in a thermodynamic sense. Atom condensates can be set to swirling by physically rotating the atom trap in which they reside. Once spun up, these atoms could subsequently be brought to rest if and when they encountered a bath of surrounding atoms, which would appropriate energy from the circulating atoms. By contrast, for the Meron phase demonstrated in the JQI simulations, the atoms are circulating because of the intrinsic magnetic forces at work, not because they had been set into motion artificially by rotating the trap. Consequently these atoms—-already in the lowest energy state possible—-cannot surrender their energy to surrounding atoms. The circulation will continue.
Observing these strange new magnetic states at ultracold temperatures will probably be the goal of future experiments.
More information: "Meron Ground State of Rashba Spin-Orbit-Coupled Dipolar Bosons," R.M. Wilson, B.M. Anderson, C.W. Clark, Physical Review Letters, , (2013). prl.aps.org/pdf/PRL/v111/i18/e185303
Journal information: Physical Review Letters
Provided by Joint Quantum Institute