Physics at the threshold of hearing

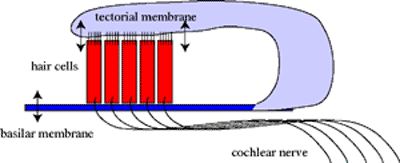
(Phys.org) —The mammalian auditory system is one of the most sensitive detectors found in nature. Two kinds of cells, the inner and outer hair cells, work together to transduce mechanical vibrations into action potentials. Sound energy is detected and transmitted by the inner hair cells, while properties like gain and frequency selectivity, are controlled by the mechanical adjustments of vibrating outer hair cells. The business end of these cells, known as the hair bundle, is composed of 30 or more stereocilia, that serve as the transducers. To date, physiologists are at odds to explain how the hair bundle can respond to mechanical stimuli whose energy is an order of magnitude below the energy level of the background thermal motion. A new study from Dolores Bozovic's lab at UCLA takes theoretical look at the mechanical vibrations of hair cells. Their analysis, recently published in Physical Review Letters, does not close the book on the noise-busting capabilities of the hair cell system, but it does provide a framework to qualitatively describe their motion, and extend current models of their behavior.

Before the mammalian state of the art evolved, animal sound systems relied on a single kind of hair cell to do it all. For that reason, scientists often use the large hair cells from the sacculus of a bullfrog for their research. By studying this low frequency auditory and vestibular organ, scientists get a first-hand look at the precursors of the mammalian inner-outer hair cell system. They have found that when these hair bundles are dissociated into a single-cell preparation, they spontaneously exhibit mechanical vibrations. These vibrations can be up to 100nm in amplitude, and require sustained energy in the form of ATP. Compared to the total length of a cell, 100nm is not huge, but it appears to be sufficient to modulate the inner-ear detection machinery. These hair cell oscillations can be driven by a sinusoidally varying stimulus, at least within a certain amplitude and frequency range.

Other researchers have shown that the spontaneous oscillations of the hair cells could be described by equations that show a Hopf bifurcation. We don't talk about Hopf bifurcations every day at Phys.org, however they do pop up in the description of dynamical systems from time to time. For example, in describing the periodicity of the heart, equations that possess a Hopf bifurcation can reveal how a system changes from a stable state to an oscillatory state. (Please see Periodic heart rate deceleration's in premature infants for further description of this.) Near a critical Hopf point in the dynamical description of the hair cells, a low-amplitude driving stimulus can produce a high-amplitude mechanical response.

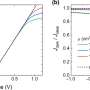
At the risk of losing the attention of a few readers, we want to impose here one more mathematical animal from the bestiary of dynamical systems—the Arnold tongue. The accompanying picture shows what an Arnold Tongue looks like in a phase space portrait. Bozovic's group was previously able to show that the phase-locked responses of hair bundles to a broad range of driving stimuli exhibited an Arnold Tongue. In their new Physical Review Letters paper, they were additionally able to show that hair bundle motion can be described by the Adler equation. This equation is commonly is used to analyze phase locking in oscillatory systems.

The group collected their data by imaging single hair bundles with a high-speed CMOS camera, and they delivered stimuli through a glass fiber. Typically, at least in mammalian outer cells, vibrations are studied by electrically stimulating the cells. Outer hair cells can remain phase locked to stimuli up to several thousand hertz. At these frequencies, electrical excitation can be delivered more practically and uniformly. The bullfrog succulus, as noted above, typically operates in the more familiar, low-frequency regime. The authors report they used a stimulus amplitude of 1.7 nm, suggesting they may be using direct mechanical stimulation here. They further report the stimulus corresponds to a force of around 0.4pN, suggesting models of the mechanical properties of cell may have been used to interpret the stimulus more flexibly.

The main results of the study were based on observations of the time evolution of the phase difference between that of the hair bundle, and that of the stimulus. They show that the system exhibits what is known in the business as a "staircase" function. The staircase structure in the phase difference is a classic signature of mode locking in a dynamical system. The authors suggest that better understanding of the effect of weak signals on spontaneous oscillations in hair cells will shed light on other phenomena, like otoacoustic emissions. These emissions are measured spontaneously in newborns—in other words, in the absence of any sound stimulus. When measured in response to a stimulus, they reliably indicate that the hearing system in a child too young to talk is intact. In tinnitus, a faulty feedback system and magnified otoacoustic emissions are often to blame. While complex at times, the application of techniques from physics to biology continues to give rewarding insight into how sensory systems operate at the threshold of noise.

© 2013 Phys.org