Math helps detect gang-related crime and better allocate police resources
(Phys.org)—Social groups in a population can lend important cues to law enforcement officials, consumer-based services and risk assessors. Social and geographical patterns that provide information about such communities or gangs have been a popular subject for mathematical modeling.
In a paper published last month in the SIAM Journal on Applied Mathematics, authors use police department records about individuals' social and geographical information to determine gang memberships.
Data on social interactions is particularly hard to come by, but in combination with geographical data, it can determine locations of specific groups in the population, such as gangs. For instance, if an individual's geographic location at a set of times is known, social interactions may be inferred by detecting people present at the same place at the same time. In this manner, hotspots at major gang locations can be determined.
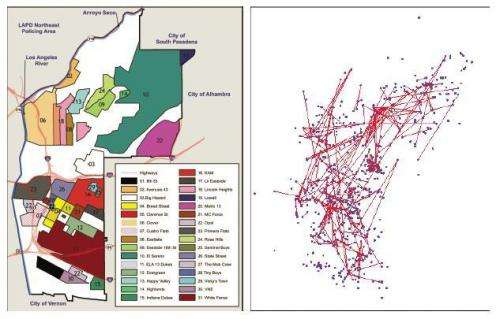
In this paper, data is used from LAPD field interview cards, which document stops by police officers of known or suspected gang members in the Hollenbeck area of Los Angeles. For each of the 748 gang members whose data is compiled, the average of all locations where they were stopped is determined, in addition to other individuals that may have been present at each stop. Due to the generally nonviolent nature of the stops, individuals stopped together are assumed to share a friendly or social connection.
A fully connected graph is constructed using this information with nodes that represent 748 individuals and an associated affinity matrix. An affinity matrix helps determine the similarity or likeness between two sets of objects or parameters. The matrix is a combination of social adjacency and an encoding function that depends on the average stop distances between individuals. In order to cluster the individuals, the authors use a technique called spectral clustering, a mathematical method used to identify groups of "similar behavior" in data. This identifies clusters in the graph based on the abovementioned social connections.
"One thing our study shows is that a clustering based purely on the locations where the people were stopped already provides clusters of over 50% purity, indicating the important role that geography plays," says lead author Yves van Gennip.
A greater amount of social data leads to improvements in clustering metrics. Since social data for such studies tends to be low, social information is extended past the current levels of sparsity by augmenting it with noise and available data on connections between members of the same gang. Such extensions of data can be particularly advantageous in tightly-controlled security settings, such as war zones. For instance, in the border regions of Afghanistan, taking into account familial, tribal and religious affiliations as well as social and economic concerns of individuals can help identify their support for insurgencies—active or passive. While intelligence information from the ground can be meager in such areas, meetings of groups of individuals can be easily observed. These methods can also be used to establish social, and hence, group interactions through geosocial information available from social media sites.
"The type of analysis undertaken in the paper can have practice applications for local law enforcement," explained one of the authors, George Tita. "While it certainly will not provide clues as to the particular individual that committed a gang-motivated crime, it can provide investigators a starting point with respect to the particular gang that might have been involved in the attack. Thus, the results of our analysis can provide a way for local police to allocate their scarce resources more strategically."
Including both social and geographic distance in models of gang violence such as this is seen to provide more comprehensive analysis – for example, in ecological models, even low levels of competition between gangs can produce sharp boundaries between gangs with a pattern of violence along borders. This "sociospatial" dimension can thus allow successful intervention to reduce gang violence. Targeted enforcement is seen not only to reduce crime in the area surrounding a gang, but also to diffuse through social networks, reducing violence among gang rivals.
"We are currently working on a much larger dataset that is similar to the one discussed in the paper," said Andrea Bertozzi, one of the authors. "The challenge is to develop algorithms that will use raw data from field interview cards from tens of thousands of people over several-years worth of events."
More information: epubs.siam.org/doi/abs/10.1137/120882093
Journal information: SIAM Journal on Applied Mathematics
Provided by Society for Industrial and Applied Mathematics