The diamond’s quantum memory

For years, quantum computers have been the holy grail of quantum technology. When a normal computer has to solve a number of problems, it can only execute them one after the other. In contrast, a quantum computer could occupy several different states at the same time – and that way it could try out different possible solutions of a problem at once, finding the correct answer much faster than a normal computer ever could. Diamonds could now bring physicists one important step closer to the quantum computer. At Vienna University of Technology, microwaves have now been coupled to the quantum states of a diamond. The results of this research project were now published in the scientific journal Physical Review Letters.
Different Quantum Technologies in One Chip
For a long time, scientists have been looking for suitable building blocks to construct a quantum computer – but without much success. Several ideas for systems which can store quantum mechanical information have been put forward, but quantum information is usually very fragile and easily destroyed. A component of a computer has to meet different criteria. It should be able to switch its state very rapidly, and it has to conserve its quantum state for a sufficient amount of time, so that calculations can be carried out. “There is no single quantum system which meets all the requirements”, Johannes Majer says. He and his team coupled two completely different kinds of quantum systems, in order to use the advantages of both sides: Microwaves and Diamonds.
Photons and Diamonds
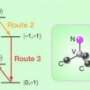
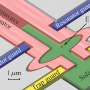
Our usual computers have a processor and a memory. The processor carries out fast calculations, the memory is supposed to remember the results for a long time. The relation between the two different quantum systems unified on one quantum chip at TU Vienna is quite similar: fast manipulations are possible due to a so called microwave resonator. Its quantum state is defined by photons in the microwave regime. This microwave resonator is coupled to a thin layer of diamond, in which quantum states can be stored.
Desirable Flaws
For jewellery, diamonds are supposed to be pure and flawless, but for quantum experiments, the opposite is required. Here, flaws in the diamond are desirable. When nitrogen atoms slip into the regular carbon structure of the diamond, the diamond becomes almost black, but it gains the ability to store quantum states. “We could show that in our quantum chip, quantum states can actually be transferred between the microwaves and the nitrogen-centers in the diamond”, Robert Amsüss (TU Vienna) explains. The more nitrogen atoms take part in this transfer of quantum information, the more stable the diamonds “memory” becomes.
Surprisingly, it turned out that also the angular momentum of the atomic nuclei can store quantum information. “This could be the first step towards a nuclear memory device”, Johannes Majer suggests. But first, the diamond quantum chip in its present form should be optimized. All the necessary parts are now there, creating the oppurtunity for reliable operations.
More information: R. Amsüss et al., Phys. Rev. Lett 107 (2011) prl.aps.org/abstract/PRL/v107/i6/e060502
Provided by Vienna University of Technology