After almost 20 years, math problem falls

For complex functions, finding global minima can be very hard. But it’s a lot easier if you know in advance that the function is convex, meaning that the graph of the function slopes everywhere toward the minimum. Convexity is such a useful property that, in 1992, when a major conference on optimization selected the seven most important outstanding problems in the field, one of them was whether the convexity of an arbitrary polynomial function could be efficiently determined.

Almost 20 years later, researchers in MIT’s Laboratory for Information and Decision Systems have finally answered that question. Unfortunately, the answer, which they reported in May with one paper at the Society for Industrial and Applied Mathematics (SIAM) Conference on Optimization, is no. For an arbitrary polynomial function — that is, a function in which variables are raised to integral exponents, such as 13x⁴ + 7xy² + yz — determining whether it’s convex is what’s called NP-hard. That means that the most powerful computers in the world couldn’t provide an answer in a reasonable amount of time.

At the same conference, however, MIT Professor of Electrical Engineering and Computer Science Pablo Parrilo and his graduate student Amir Ali Ahmadi, two of the first paper’s four authors, showed that in many cases, a property that can be determined efficiently, known as sum-of-squares convexity, is a viable substitute for convexity. Moreover, they provide an algorithm for determining whether an arbitrary function has that property.

Downhill from here

On the first paper, Parrilo and Ahmadi were joined by John N. Tsitsiklis, the Clarence J. LeBel Professor of Electrical Engineering, and Alex Olshevsky, a former student of Tsitsiklis’ who’s now a postdoc at Princeton University. According to Etienne de Klerk, a professor in the Department of Econometrics and Operations Research at Tilburg University in the Netherlands, the revelation that determining convexity is NP-hard is “not only interesting but quite surprising.”

"If you take any textbook of optimization that we use to teach undergrads, it will typically start, 'Let the complex optimization be given,'" de Klerk says. "All the functions are convex functions." The MIT researchers' work, he adds, will "make you view the world of optimization in a slightly different way."

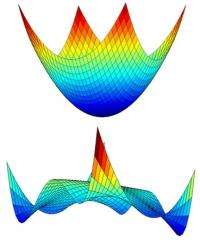
To get a sense of why convexity is so useful, imagine an airplane in flight, and suppose that you have a function that relates its altitude and speed to the amount of fuel it will consume — naturally, a quantity you’d want to minimize. If the function is convex, its graph — which is three-dimensional — looks like a big bowl, and at the bottom is the combination of altitude and speed that minimizes fuel consumption. All the plane’s control algorithm has to do is find a new altitude and speed that are down the slope of the bowl, and it knows it’s heading in the right direction. But if the function isn’t convex, the graph might look like a mountain range. The minimum value might lie across several peaks and basins, and locating it could be too time consuming to do on the fly.

Squaring off

Of course, the types of functions that real control algorithms have to deal with are much more complex. But that only heightens the advantage of convexity: It guarantees that you can make an informed decision using only limited, local information. “In control theory, there’s been a big shift in recent years toward doing online optimizing,” Parrilo explains. “Now, because we have such big computational power, you can afford controllers that do things that are a lot more complicated. They actually solve optimization problems on the fly.” But, Parrilo says, “if you want to do this, you need some kind of guarantee that the decision that you’re going to take is going to be optimal, or close to optimal, and also that you can do this in a certain period of time.” Convexity provides that guarantee.

Since the circumstances surrounding the operation of an electromechanical system are constantly changing, so are the functions that describe the system’s optimal state. It would be nice to be able to tell in advance whether those functions are convex, but alas, the MIT researchers have shown that that’s not always possible.

But Parrilo and Ahmadi also proved that, for polynomial functions with few variables or small exponents, convexity is the same thing as sum-of-squares convexity, which is easy to check. (“Sum of squares” just means that a polynomial, like x² – 2xy + y² + z², can be rewritten as the sum of expressions raised to the power of two — in this case, (x – y)² + z².)

Moreover, Ahmadi points out, in order to prove that sum-of-squares convexity is not always the same thing as convexity, he and Parrilo had to come up with some bizarre counterexamples that are unlikely to arise in most engineering contexts. “If you have few enough variables, say less than five or six, it’s not easy to find examples where it doesn’t work,” Ahmadi says. “So it’s pretty powerful, at least for reasonable problems.”

Provided by Massachusetts Institute of Technology