Maximum overhang, optimum reward

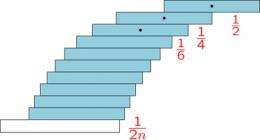
Maximum Overhang—by Mike Paterson of the University of Warwick, Peres, Mikkel Thorup of AT&T Labs, Peter Winkler of Dartmouth College, and Uri Zwick of Tel Aviv University—builds on a paper titled Overhang, by Paterson and Zwick, the other paper cited in the prize. Together, the papers revisit a classic problem in mathematics: how to stack blocks on a table to achieve the maximum possible overhang—the farthest horizontal distance from the edge of the table.

“Like most people,” Peres recalls, “I had thought it seemed sensible to stack just one block at each level, which leads to the classical solution. I did not think of other possibilities. It’s good to retain some healthy skepticism of accepted wisdom.”

The David P. Robbins Prize is awarded for novel research in algebra, combinatorics, or discrete mathematics. The winning paper must be on a topic that is broadly accessible, written in a way that provides a simple statement of the problem and with clear exposition of the work. It certainly helped that the maximum-overhang problem has been a source of fascination for more than 150 years.

“Initially, it's surprising,” Peres says, “that it is possible at all to get farther than one block of overhang away from the edge of the table without any glue. Once one finds the classical solution, related to the harmonic series, it seems so beautiful and satisfying. It seems counterintuitive that one could do much better—that’s one source of fascination.”

Enlarge

A classic stack of 30 blocks (in orange) compared to the same number of blocks configured as a jagged wall (in gray) held stable by counterweights (in blue).

The topic fits into a general theme of crucial importance at Microsoft Research: constrained optimization.

“Optimization problems occur repeatedly in applications,” Peres says. “Scheduling jobs to different machines to minimize waiting times, deciding how frequently to crawl different websites when refreshing a search-engine index, setting up a network that will connect a set of processors at minimal cost—these can all be recast as optimization problems. Thus, developing new tools and insights pertinent to optimization is a key concern in the Theory Group at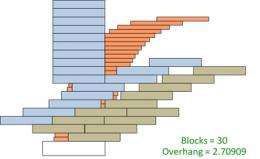 Microsoft Research.”

The prize-winning papers offer a different approach, first, by stacking blocks to resemble a badly built wall, with holes, jagged edges, and a solid stack that acts as a counterweight. This extends the overhang beyond what the classic stack can achieve using the same number of blocks.

Then, to push results even farther out, the team sought a solution that optimized for a large number of blocks and devised a radical shape that yielded exponentially better results than the classic approach.

It was Zwick who then noticed a connection between the block-stacking problem and “random walk,” a fundamental tool used in areas of computer science such as web algorithms, distributed networks, and theory.

“Since I have worked on many problems involving random walks,” Peres says, “he approached me to help expand on the work. The principles of statics allowed us, together with our co-authors, to relate the overhang problem to the following, seemingly unrelated problem: Starting with a unit of mass at the origin, how many moves does it take to move half the mass to distance n, where in each move a node k between -n and n is chosen and the mass at k is split evenly between k-1 and k+1. It is easy to see that order n3 moves suffice, and a key step of the Maximum Overhang paper was to show that this number of moves is also necessary.”

In its citation, the MAA applauds the researchers for presenting both problem and arguments in a manner accessible even to math undergraduates, despite the inherently complex mathematics of the solution. For Peres, this criterion for the award is significant.

“It’s always great to get recognition,” he says. “But this award, besides being about mathematics, is also about exposition. As mathematicians, I think it is very important that we think more often about outreach and connecting to other people with different interests and motivations, to share our excitement and love of mathematics.”

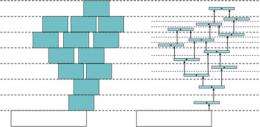
The papers’ many illustrations are effective in communicating the work, a strategy familiar to Peres, whose webpage features beautiful, computer-generated images of mathematical constructs, courtesy of talented colleagues.

Enlarge

An "oil lamp" stack, whose results astonished even the researchers.

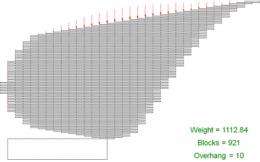
“I think images and simulations can play a major role in motivating mathematical research,” he says. “Those images hold an intrinsic beauty for both mathematicians and outsiders. You often hear about the beauty of mathematics, and, for me, some of that beauty is due to the unexpected patterns you find. Their mechanism gives no indication of why these patterns happen, so a lot of the math we do tries to explain the patterns. So far, the patterns are winning, because we can only explain a small part of what we see in the images. We are still very much challenged by them.”

The ongoing challenge of his research is one of the things Peres relishes most in his life.

“I enjoy cracking a hard problem,” he says, “preferably by bringing in perspectives from unexpected areas. I also love mentoring talented students, helping them become mathematicians. Best of all is when I can combine both these endeavors.”

He admits that he enjoys work so much he doesn’t spend enough time on hobbies such as hiking and swimming. Rather ruefully, he recalls overhearing his son, 6 at the time, asking a friend: “Do you have a religion? You know, a religion, like Jewish, or Christian, or Mathematics?”

“My wife would take our sons to synagogue on Saturday mornings,” he explains. “I used the time to go to the office and think about math. So he must have figured that whatever you choose to do on your Saturday mornings, that’s your religion.”

Enlarge

The proof in Maximum Overhang uses ideas from random walks: Start with mass 1 at the origin. How many mass-balanced splits are needed to get half the mass to distance d?

Peres has regarded the world through the lens of mathematics from a young age. His paternal grandfather, Julius Posener, was a physicist, educator, and violinist who took the time to discuss with Peres the mathematics of music and how mathematicians of the Renaissance solved cubic and quartic equations.

“I was 12,” Peres recalls, “when he explained to me the geometry of complex numbers. I remember emerging into the sunlight and thinking that now I had a new way to understand the world—and it would never look the same again. At 13, I inherited my grandfather’s scientific books, many of them probability books, and by 14, I was pretty sure I wanted to be a mathematician.”

Equally crucial to the way Peres regards his work has been the influence of his maternal grandmother.

“Though not formally educated in math,” Peres says, “she was a calculating whiz. Her favorite saying was, ‘Why should I be surprised when I can simply disbelieve?’ She taught me the virtues of skepticism—and also of keeping an open mind.”

The work on the maximum-overhang problem epitomizes a situation in which skepticism and an open mind have challenged conventional wisdom and have delivered new results.

“The point is that we need to be willing to re-examine some natural assumptions,” Peres says. “It seems so natural to stack each block one level above the other. Why would you place several blocks at the same level? If you follow that natural assumption, then yes, the classic solution is the best one.

“But if you think outside the box, you can obtain unexpected insights. I think the lesson, the whole philosophical point, is about the nature of problem solving. It’s about finding and re-examining the hidden assumptions we make before we even start to think seriously about a problem.”

Source: Microsoft Corporation