Beating the competition: Scientists discover how the size of networks can skyrocket

Imagine the following scenario: In your sports team you get to know a new player and arrange to go out and see a movie on the next weekend. The new team member brings along three friends - and suddenly by adding one new contact, your own circle of friends has grown by four people. Growth processes of this sort occur in many networks: Neurons in the brain constantly establish new connections, websites link to each other and a person travelling infected with influenza creates a network of infected places with each intermediate stop. From a scientist's point of view, such growth processes are still poorly understood: How does a network change when single links are added? How quickly does a network grow in this way?

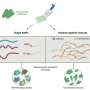
To answer these questions, the scientists from Göttingen tracked the growth of networks link by link. A new connection, however, can not only add one new element. It can also merge two networks (as in the example in the sports team above). The researchers focused on a special form of network growth that introduces a form of competition between possible links: If several new connections are possible, only the one connection is created: the one that results in the smallest new network (see Figure 1). "There is evidence, that growing networks of neurons at first prefer forming small groups and thus roughly follow the growth process we discuss", says Jan Nagler, staff researcher at the University of Göttingen and the MPIDS.

Enlarge

The growth process of the networks described in the study. Left: In the beginning, only few elements joint to form many small networks. Middle: In the intermediate phase several mid-sized networks have been created. Right: In the end almost all elements are connected in one large network. Credit: Max Planck Institute for Dynamics and Self-Organization

“In our study we zoomed in on an intermediate growth phase. This phase arises after the elements have begun to sporadically connect into small groups, but before the entire system is linked”, explains Marc Timme, head of the Network Dynamics Group at MPIDS. How do the many small networks link to form a whole? Are several large networks created at the same time or does one dominant network develop that towers above the others? In addition to performing computer simulations, the Göttingen researchers were for the first time able to derive mathematical expressions that describe this growth phase link by link.

The scientists found that after a certain number of new links, a sudden growth spurt occurs: The size of the largest network within the system is enhanced dramatically. “With respect to the size of the system, this jump is more dramatic in small systems than in large ones”, says Nagler. However even in systems that consist of a huge number of elements – comparable for example to the number of neurons in the brain – the size of the largest network can double. “At first, many networks of moderate size develop in this way”, says Timme. Thus, a dominant spanning network emerges only at a late stage in the growth process.

In a next step, the researchers now want to identify which forms of competition in natural systems from biology and physics imply this rapid growth and study the consequences of these growth spurts.

More information: Nagler, Anna, Marc Timme, "Impact of Single Links in Competitive Percolation." Nature Physics online, 16. January 2011

Provided by Max-Planck-Gesellschaft