February 26, 2010 feature
Quantum measurement precision approaches Heisenberg limit
(PhysOrg.com) -- In the classical world, scientists can make measurements with a degree of accuracy that is restricted only by technical limitations. At the fundamental level, however, measurement precision is limited by Heisenberg’s uncertainty principle. But even reaching a precision close to the Heisenberg limit is far beyond existing technology due to source and detector limitations.
Now, using techniques from machine learning, physicists Alexander Hentschel and Barry Sanders from the University of Calgary have recently shown how to generate measurement procedures that can outperform the best previous strategy in achieving highly precise quantum measurements. The new level of precision approaches the Heisenberg limit, which is an important goal of quantum measurement. Such quantum-enhanced measurements are useful in several areas, such as atomic clocks, gravitational wave detection, and measuring the optical properties of materials.
“The precision that any measurement can possibly achieve is limited by the so-called Heisenberg limit, which results from Heisenberg's uncertainty principle,” Hentschel told PhysOrg.com. “However, classical measurements cannot achieve a precision close to the Heisenberg limit. Only quantum measurements that use quantum correlations can approach the Heisenberg limit. Yet, devising quantum measurement procedures is highly challenging.”
Heisenberg's uncertainty principle ultimately limits the achievable precision depending on how many quantum resources are used for the measurement. For example, gravitational waves are detected with laser interferometers, whose precision is limited by the number of photons available to the interferometer within the duration of the gravitational wave pulse.
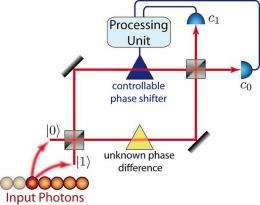
In their study, Hentschel and Sanders used a computer simulation of a two-channel interferometer with a random phase difference between the two arms. Their goal was to estimate the relative phase difference between the two channels. In the simulated system, photons were sent into the interferometer one at a time. Which input port the photon entered was unknown, so that the photon (serving as a qubit) was in a superposition of two states, corresponding to the two channels. When exiting the interferometer, the photon was detected as leaving one of the two output ports, or not detected at all if it was lost. Since photons were fed into the interferometer one at a time, no more than one bit of information could be extracted at once. In this scenario, the achievable precision is limited by the number of photons used for the measurement.
As previous research has shown, the most effective quantum measurement schemes are those that incorporate adaptive feedback. These schemes accumulate information from measurements and then exploit it to maximize the information gain in subsequent measurements. In an interferometer with feedback, a sequence of photons is successively sent through the interferometer in order to measure the unknown phase difference. Detectors at the two output ports measure which way each of the photons exits, and then transmit this information to a processing unit. The processing unit adapts the value of a controllable phase shifter after each photon according to a given policy.
However, devising an optimal policy is difficult, and usually requires guesswork. In their study, Hentschel and Sanders adapted a technique from the field of artificial intelligence. Their algorithm autonomously learns an optimal policy based on trial and error - replacing guesswork by a logical, fully automatic, and programmable procedure.
Specifically, the new method uses a machine learning algorithm called particle swarm optimization (PSO). PSO is a “collective intelligence” optimization strategy inspired by the social behavior of birds flocking or fish schooling to locate feeding sites. In this case, the physicists show that a PSO algorithm can also autonomously learn a policy for adjusting the controllable phase shift.
As Hentschel and Sanders show, after a sequence of input qubits have been sent through the interferometer, the measurement procedure learned by the PSO algorithm delivers a measurement of the unknown phase shift that scales closely to the Heisenberg limit, setting a new precedent for quantum measurement precision. The new high level of precision could have important implications for the gravitational wave detection.
“Einstein’s theory of General Relativity predicts gravitational waves,” Hentschel said. “However, a direct detection of gravitational waves has not been achieved. Gravitational wave detection will open up a new field of astronomy that augments electromagnetic wave and neutrino observations. For example, gravitational wave detectors can spot merging black holes or binary star systems composed of two neutron stars, which are mostly hidden to conventional telescopes.”
More information: Alexander Hentschel and Barry C. Sanders. “Machine Learning for Precise Quantum Measurement.” Physical Review Letters 104, 063603 (2010). DOI:10.1103/PhysRevLett.104.063603
Copyright 2010 PhysOrg.com.
All rights reserved. This material may not be published, broadcast, rewritten or redistributed in whole or part without the express written permission of PhysOrg.com.