Artificial magnetic fields for light could illuminate correlated quantum systems

(PhysOrg.com) -- In general, the field of many-body physics involves the interactions and collective behavior of large numbers of particles. Scientists have made significant progress in exploring this field, which has led to applications in condensed matter physics, nuclear physics, and astrophysics. However, one challenging area that remains is understanding many-body systems on the quantum level.

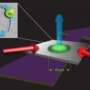
In a recent study, a team of physicists, J. Otterbach, et al., from the University of Kaiserslautern in Germany and Vilnius University in Lithuania have proposed a new method for probing strongly correlated quantum systems. They show that it is possible to create artificial magnetic fields for stationary light using a uniformly rotating medium, such as a rotating optical lattice or other system. In this scenario, light behaves as a massive quantum particle in a magnetic field. The physicists predict that this system could enable scientists to study a variety of single- and many-particle quantum effects.

The new design involves the use of photonic quasiparticles called stationary-light polaritons (or “heavy light”). Quasiparticles were recently suggested as a tool for investigating correlated quantum systems. In general terms, a quasiparticle can be thought of as a combination of a real particle and its surrounding environment. For instance, stationary-light polaritons are a superposition of photonic and matter excitations in the surrounding space. Unlike charged particles such as electrons, which are forced by a magnetic field into circular orbits, neutral particles such as quasiparticles do not couple with magnetic fields.

“If one wants to see effects similar to electrons in solid state physics related to the presence of a magnetic field, one has to create an ‘effective’ magnetic field,” coauthor Michael Fleischhauer from the University of Kaiserslautern told PhysOrg.com. “We showed how to do this for ‘heavy light’ quasiparticles.”

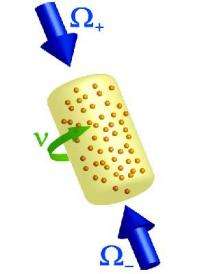
In the scientists’ proposed design, stationary-light polaritons are created in a rotating ensemble of atoms driven by counterpropagating lasers. The system consists of four states - two excited atomic states and two atomic ground states - which are coupled together in a closed configuration by four light fields with opposite polarizations. The scientists explain that the rotation of the light fields is similar to cold rotating gases that are used to trap cold atoms, except that the new system uses quasiparticles instead of atoms. Here, the polaritons can be described as quantum particles (either Schrodinger or two-component Dirac particles) in magnetic fields, and their effective mass can be adjusted by two control lasers.

“Ideally, one wants to make the effective magnetic field as strong as possible,” Fleischhauer said. “For stationary-light quasiparticles, this [strength] can potentially be higher than what can be achieved for cold atoms.”

Fleischhauer predicts that these artificial magnetic fields should be strong enough to allow researchers to study highly correlated quantum states, such as the fractional quantum Hall effect. Further, there are numerous experimental systems available today that could be used to implement this scheme.

“In order to see the quantum effects one needs interactions,” he explained. “The magnetic field is, however, a necessary and important prerequisite. Its action leads (without interaction) to largely degenerate quantum states. … If interactions are switched on, the lowest energy state of the system becomes a very interesting many-body state with non-local quantum correlation. This is also the origin of the so-called fractionalized quantum Hall effect. These effects were interesting and important enough for two Nobel prizes (the integer quantum Hall effect by K. von Klitzing in 1985; and the fractional quantum Hall effect by R. Laughlin, H. Stoermer, and D. Tsui in 1998).”

Copyright 2010 PhysOrg.com.
All rights reserved. This material may not be published, broadcast, rewritten or redistributed in whole or part without the express written permission of PhysOrg.com.