Math professor discovers chaos on a 'fluid trampoline'

(PhysOrg.com) -- A water drop placed on a soap film that vibrates up and down may bounce as if on a trampoline -- but it's much more than that, according to MIT mathematicians who say the "fluid trampoline" is the simplest fluid example of chaos theory ever explored.
MIT math professor John Bush and visiting student Tristan Gilet built the system in the Applied Math Laboratory, then demonstrated that the drop bouncing may be accurately described with a single simple equation. They report their findings in an upcoming issue of Physical Review Letters.
Their study builds upon the pioneering work of the late Edward Lorenz, an MIT meteorologist who in 1963 discovered chaos in a simplified mathematical model of the atmosphere, now called the Lorenz equations. Known as the father of chaos theory, Lorenz passed away in April 2008 after a distinguished career in MIT's Department of Earth, Atmosphere and Planetary Sciences.
The trademark of chaotic systems is their sensitivity to initial conditions. Any uncertainty in the initial state of a chaotic system will soon be amplified, leading to a loss of predictive power over the system. The chaotic nature of the Earth's atmosphere is responsible for the shortcomings of weather forecasts, which are notoriously untrustworthy beyond a few days.
Since Lorenz's early work, chaos has been discovered in a wide variety of complex systems, from the beating heart to population dynamics, from planetary orbits to the stock market. An interesting philosophical question arises, says Bush: "What is the simplest physical system that exhibits chaotic behavior? What are the minimum ingredients for chaos?"
In the 1970s, MIT math professors Lou Howard and Willem Malkus developed the first mechanical chaotic oscillator in the Applied Math Laboratory, a water wheel whose motion is precisely described by the Lorenz equations. The original water wheel consists of a series of perforated Dixie cups fixed to a tilted wheel: When the cups are filled from above, the wheel trajectory may spin in an unpredictable, chaotic
fashion.
Subsequently, chaos has been observed and studied in a number of simple systems, including a bouncing rubber ball, the double pendulum and the dripping faucet. While the latter system is the simplest fluid oscillator to study experimentally, Bush points out that the fluid trampoline is the simplest when one considers both ease of experiment and theory.
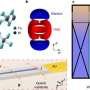
The form of bouncing on the fluid trampoline depends on the amplitude and frequency of the soap film vibration. At low amplitude, the drop bounces with the period of the forcing. Progressively increasing the amplitude leads to the bouncing period doubling then quadrupling. Ultimately, chaos emerges via a so-called period-doubling cascade. The authors demonstrate that the trajectory of the bouncing drop is accurately described by a single second-order differential equation that allows them to rationalize all of the observed bouncing behavior, including the period-doubling transitions to chaos.
Their study is the latest milestone in MIT's long association with chaos theory. Says Bush, "We have brought chaos back to its fluid mechanical roots at MIT."
Gilet, a graduate student from the University of Liege in Belgium, was visiting MIT thanks to the financial support of the FNRS/FRIA and the Belgian government.
Provided by MIT