Physicists Build a Quantum Gambling Machine

Quantum gambling machines may not be popping up at futuristic casinos any time soon, but the devices could have other uses – such as enabling physicists to study game theory in situations where cheating is impossible.

That’s because, in the quantum domain, opponents can always figure out what choice the other made when the game is over, thanks to superpositions of their actions. In the classical version of the “Pick the Winning Box” game, for example, a casino operator hides a ball in either box A or box B, and a player guesses the box that contains the ball in order to win. If the game were played remotely, the casino operator could easily lie about which box the ball was in if the player chose the winning box. Or, if the boxes were with the player, he could cheat by claiming that he found the ball when he did not.

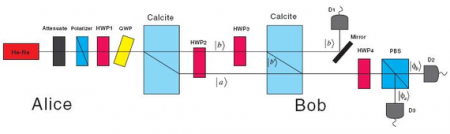
But in quantum gambling, this kind of cheating is impossible, opening up the possibility for remote gambling. Researchers Yong-Sheng Zhang and colleagues from the University of Science and Technology of China have built such a quantum gambling machine using optical elements, which they describe in a recent issue of Europhysics Letters.

“As far as I know, this is the first demonstration of a quantum gambling machine since L. Goldenberg et al. presented it in 1999,” Zhang told PhysOrg.com. “It is a toy model of applications of quantum mechanics, and it may be used in real gambling.”

First, the machine generates a photon, which has a definite polarization state of either vertical or horizontal. Then, to represent Alice the casino operator, a half wave plate transfers the photon into a superposition of horizontal and vertical states. In an equally distributed state, the photon would be half vertically polarized and half horizontally polarized. Then, a beam splitter splits the photon beam into beam A and beam B. At the end of the machine, there will be a 50-50 chance of the photon ending up in the player Bob’s “box” (his detector, B) or Alice’s detector, A.

But the game offers other variables. To alter that 50-50 probability, for instance, Alice has the option of preparing a biased superposition state – for example, one that is more vertically polarized than horizontally polarized, or vice versa. Then, there would be a smaller chance that the photon would end up in Bob’s detector than in Alice’s detector.

However, Bob has another option besides passively waiting to see if his detector gets the photon. Like Alice, Bob also has a half wave plate, and he can use it to split his beam B into two parts according to a splitting parameter of his choice. Then, one path of his split beam, B’, is superposed back with beam A. He would probably choose a higher splitting parameter if he thought that Alice had chosen a superposition state that was highly biased against putting the photon in his beam. In a sense, splitting his beam B gives Bob a second chance of winning, and – depending on the bet – winning a greater amount.

If Bob’s detector doesn’t get the photon, then it will go to either Alice’s detector A or a third detector, B’. If Bob bet on the photon landing in detector A, and it does, then Bob wins a previously agreed sum, while a photon in detector B means Bob loses that sum (i.e. he chose the wrong box, in the classical analogy). Similarly, if he had bet on detector B, and the photon was detected there, he would win that bet, too. But he cannot bet on detector B’.

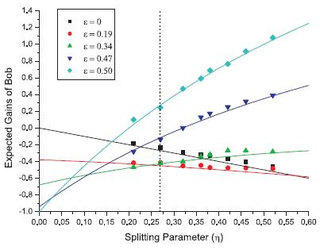
So Bob and Alice both have sway over where the photon ends up. If Bob chooses a high splitting parameter and Alice had chosen a greatly biased superposition state (so that she increased the chance of having the photon in beam A), the photon would be more likely to go to detector A than B’, and Bob would win. But if Alice had chosen a more equal superposition state (so that beam B was just as likely to have the photon), the photon would be more likely to go to detector B’ than detector A, and Bob would lose. In this case, Bob would have been better off choosing a lower splitting parameter, or not splitting his beam at all.

In a sense, Bob’s choice of his splitting parameter depends on how equally he thinks Alice prepared the original photon. The researchers figured out the optimal splitting parameter for Bob that would make him the most money for any superposition state that Alice chooses, for a game when Bob’s winnings would be 5 for detector A and 1 for detector B (and losing the same amount if his bet is wrong). They also found that Bob has a greater chance of losing than winning.

As the researchers explain, this demonstration of a quantum gambling machine shows that quantum mechanics could have interesting implications in traditional game theory. For instance, quantum gambling might reveal insights into the foundations of game theory, survival games, and quantum communication. And quantum mechanics could also ensure fairness in remote gambling.

“It is not clear how this gambling machine can affect people’s lives,” Zhang said. “However, with more and more things being used in gambling and trade [Super Tuesday: Markets Predict Outcome Better Than Polls, Scientific American, Feb. 2008], it can be conjectured that a quantum gambling machine whose security is guaranteed by the laws of physics may have some role in the future.”

More information: Zhang, P.; Zhang, Y.-S.; Huang, Y.-F.; Peng, L.; Li, C.-F., and Guo, G.-C. “Optical realization of quantum gambling machine.” Europhysics Letters, 82, (2008) 30002.

Copyright 2008 PhysOrg.com.
All rights reserved. This material may not be published, broadcast, rewritten or redistributed in whole or part without the express written permission of PhysOrg.com.