March 25, 2016 feature
Mathematician finds his 'new' solution to Poisson formula problem buried in 1959 paper
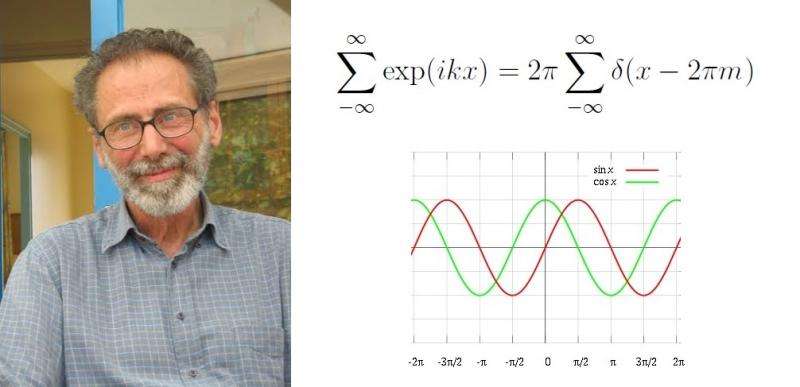
(Phys.org)—As Yves Meyer was getting ready to publish a detailed mathematical proof that he had spent months working on, he decided do a final search of the existing literature. In the reference list of one of the papers he had just peer-reviewed, he noticed what he describes as a "bizarre" paper published in 1959 by Andrew Paul Guinand. Upon further investigation, he was shocked to discover that Guinand had formulated the exact same proof to solve the same problem that Meyer had been working on, though the solution had remained deeply buried and completely forgotten.
Meyer, a Professor Emeritus at the École Normale Supérieure de Cachan, accordingly revised and published his paper, which appeared just a few weeks ago in the Proceedings of the National Academy of Sciences. In his work, he proves that there is not just one, but many Poisson summation formulas, using a simpler solution than was previously known.
Meyer—who has spent his career making fundamental contributions to wavelet theory and number theory, and recently won the Gauss Prize—explains that at first he was somewhat embarrassed that someone else had made the same discovery many decades earlier. However, he also interprets the experience as an example of a more universal pattern: that all of human discovery builds on what comes before.
"Suddenly I understood what I have been steadily doing in my scientific life," Meyer told Phys.org. "I was transmitting a heritage. Today I can express my gratitude to Guinand, who was a great person, both as a human being and as a mathematician."
Not just one Poisson formula
Meyer has spent much of his career investigating the mathematical properties of oscillations. One question that arises is, what happens when large numbers of sines or cosines interfere with one another? This interference occurs in many physical scenarios, such as X-ray crystallography, a technique used to study crystals. The Poisson formula is the tool that researchers use to understand this interference.
The original Poisson formula, which was discovered in the early 1800s by Siméon Denis Poisson, equates two sums. The first sum involves an infinite number of trigonometric functions being added together, and the second one an infinite number of "spikes" being added. For a simple example, the first sum is ½ + cos(x) + cos(2x) + cos(3x) + cos(4x) +…. This sum can add to either zero or infinity, and which answer you get depends on the value of the variable x. In this example, when x is any number that is not a multiple of 2π, then the sum is zero, corresponding to destructive interference. Meyer explains that this situation can be thought of as all of the numbers cos(x), cos(2x), cos(3x),… being evenly situated around 0, so that even though there is an infinite number of numbers, when added, they all cancel each other out.
On the other hand, when the variable x is some multiple of 2π, then 1 = cos(x) = cos(2x) = cos(3x)…, so their sum spikes to infinity, corresponding to constructive interference. This sum of spikes is the second sum.
The big question that Meyer was investigating was whether other Poisson formulas might exist with completely distinct arithmetic properties. For a long time, mathematicians believed that the original formula was the only Poisson formula.
But then in late 2015, Meyer was reviewing a new paper by Nir Lev and Alexander Olevskii that proved that other Poisson formulas do indeed exist. This paper inspired Meyer's new proof, and was also the paper that referenced Guinand's 1959 paper—though of course Lev and Olevskii had not noticed the more elegant proof buried within this paper.
"I was enthused by Lev and Olevskii's discovery, and I lectured on it with Olevskii's permission," Meyer said. "Then a much simpler solution unconsciously came to my mind. I wrote a detailed proof. Before publishing it, I wanted to check the existing literature. In the reference list of the Lev and Olevskii article, a bizarre paper by A.P. Guinand attracted my attention. This odd paper was published in 1959. I went to a mathematical library and I was overwhelmed by surprise and shame. Indeed, Guinand used my solution to solve the problem raised by Lev and Olevskii. You had to read between the lines in Guinand's article to check what I am saying."
Throughout his paper, Meyer gives credit to Guinand and even names one of Guinand's ideas after the late mathematician, calling it "Guinand's distribution."
A story that continues to be written
Although in one sense it is surprising that one of the same problems in modern mathematical research was being worked on more than half a century ago, in another sense that is just the nature of the field. Meyer explains that he collaborated with and admired many highly regarded mathematicians throughout his career (Alberto Calderón, Alexander Grossmann, and Jean Morlet, among others), and that their ideas are continually being reanalyzed, reshaped, and sometimes even applied to new innovations.
One prominent example of a new application can be found in the recent detection of gravitational waves. The algorithm used in the discovery contains something called the "Meyer wavelet," which Meyer proposed 25 years ago, and work by other mathematicians has also played an important role. Overall, wavelet theory (which Meyer helped develop over the past several decades) has applications in analyzing data from audio signals, images, electronic signals, and in general to extract information from many different kinds of signals.
All of these recent developments have their roots in past research—often, Meyer explains, from the distant past.
"And the story does not end there," Meyer said. "Today I am continuing my research on Olevskii's problem. I discovered an ancient paper by my former advisor Jean-Pierre Kahane. It is a joint work with Sjolem Mandelbrojt. Then I went further into the past and could trace everything back to the Epstein zeta function, which was discovered and studied in 1903. But this is another story."
More information: Yves F. Meyer. "Measures with locally finite support and spectrum." PNAS. DOI: 10.1073/pnas.1600685113
Journal information: Proceedings of the National Academy of Sciences
© 2016 Phys.org