December 17, 2013 report
Some Polynesian islanders combined binary and decimal math
(Phys.org) —When we think of binary math, we think of computers. A number system with only two digits makes calculations quick and easy. However, binary numbers can be very long and, therefore, unwieldy. While binary numbers might be great for machines, decimal numbers are shorter and more comfortable for people to use. A system that combines the benefits of base 2 and base 10 could be ideal. Andrea Bender and Sieghard Beller of the University of Bergen in Norway have discovered that the Mangarevans of French Polynesia used such a hybrid system at least 500 years ago. Their research appears in the Proceedings of the National Academy of Sciences.
Gottfried Leibniz introduced binary numbers to the western world in the 18th century, proclaiming their practical advantages and pointing out that learning binary addition and multiplication tables would be much easier than learning decimal ones. Nevertheless, while a binary system became the basis for computers, binary numbers never became part of everyday western life. We are used to a decimal system—we have 10 fingers and 10 toes, after all— and while a base 2 system may have its advantages, those long strings of 1s and 0s seem unnatural.
Hundreds of years ago, the people of the island of Mangareva in French Polynesia developed a way to use binary math while eliminating the problem of every long numbers. They did this by combining a binary with a decimal system. Bender and Beller learned about this system when studying the Mangarevan language and Mangarevan historical records.
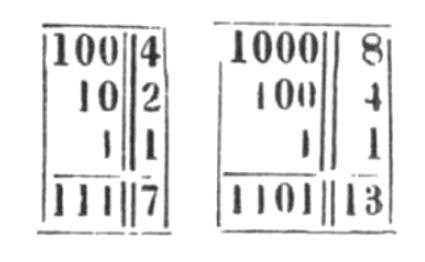
The Polynesians who arrived in Mangareva over 1,000 years ago used a decimal system, as other Polynesians did. However, by A.D. 1450, the Mangarevans were using a system that combined base 10 and base 2. In the Mangarevan language, there are words for the numbers 1 through 9, as with all decimal systems. After that, the system turns into a binary one, with words for 10, 20, 40 and 80.
This mixed system simplifies mental arithmetic but doesn't make it hard to express large numbers. The researchers believe that the hybrid system played a useful role in Mangarevan culture, where people often traded large quantities of goods or offered them as tribute. The Mangarevans used their system to count objects considered highly valuable, including coconuts, fish and octopuses.
Today, the Mangarevan language risks extinction. The number of speakers has decreased from about 1,600 in 1987 to 600 in 2011, despite the island's population remaining stable. The Mangarevans have adopted the Arabic digits and the decimal counting system used by much of the world.
More information: Mangarevan invention of binary steps for easier calculation, PNAS, Published online before print December 16, 2013, DOI: 10.1073/pnas.1309160110
Abstract
When Leibniz demonstrated the advantages of the binary system for computations as early as 1703, he laid the foundation for computing machines. However, is a binary system also suitable for human cognition? One of two number systems traditionally used on Mangareva, a small island in French Polynesia, had three binary steps superposed onto a decimal structure. Here, we show how this system functions, how it facilitated arithmetic, and why it is unique. The Mangarevan invention of binary steps, centuries before their formal description by Leibniz, attests to the advancements possible in numeracy even in the absence of notation and thereby highlights the role of culture for the evolution of and diversity in numerical cognition.
Journal information: Proceedings of the National Academy of Sciences
© 2013 Phys.org