July 8, 2013 feature
Two papers investigate the thermodynamics of quantum systems
(Phys.org) —As one of the pillars of the natural sciences, thermodynamics plays an important role in all processes that involve heat, energy, and work. While the principles of thermodynamics can predict the amount of work done in classical systems, for quantum systems there is instead a distribution of many possible values of work. Two new papers published in Physical Review Letters have proposed theoretical schemes that would significantly ease the measurement of the statistics of work done by quantum systems.
The papers, "Extracting Quantum Work Statistics and Fluctuation Theorems by Single-Qubit Interferometry" led by Vlatko Vedral, a physics professor at the University of Oxford in the UK and the National University of Singapore; and "Measuring the Characteristic Function of the Work Distribution" led by the Quantum Technology Group at Queen's University in Belfast, UK, both investigate the thermodynamics of quantum systems.
Traditionally, the principles of thermodynamics have applied only to classical systems because of the inherent differences that arise at the quantum level.
"Take a classical system, and subject it to a transformation, which might result in some work done on/by the system," Mauro Paternostro, an associate professor (reader) and co-author of the work signed by the Belfast team, explained to Phys.org. "Now, consider a quantum mechanical system subjected to an analogous quantum evolution. As quantum mechanics is inherently probabilistic, you do not have a definite, well defined value of work. On the contrary, you end up with a statistical distribution of possible values of work done on/by the system. Each value is associated with a possible 'trajectory' followed by the quantum system in its evolution due to the transformation. The expectation value of such a distribution is something close to the classical value of work performed on/by the analogous classical system. But the fact that it's a distribution (a quantum one!) makes it inherently different from classical mechanics.
As Paternostro explained, the quantum work distribution is very important because it's a key quantity in the framework of non-equilibrium quantum statistical mechanics, which is a formalism that describes the statistical and thermodynamical properties of a quantum system brought out of equilibrium. In addition, quantum analogies of classical fluctuation relations can be formulated in terms of the work distribution.
"So far, accessing the work distribution has found only limited success," Paternostro said. "Experimentally, [our proposal] would be a significant result, as the experimental determination of the work distribution would allow the assessment of quantum fluctuation relations, and thus the establishment of an experimental ground for quantum thermodynamics. Although some proposals have been put forward in the past, these were either too difficult, technically, or valid only in special cases.
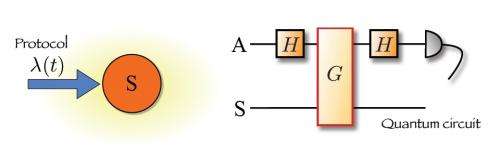
"Our two proposals (the one by the Oxford group led by Prof. Vedral and the one from my group) managed to bypass such hindrances to (a) assess general processes, not just special cases, and (b) offer the promise for experimental implementability, as they are based on something known as phase-estimation strategies, which have found successful demonstrations in the past."
The scheme proposed by the Belfast team involves an ancilla-based measurement that can be applied to a micro- or nano-mechanical oscillator. On the other hand, Vedral and his coauthors' proposal uses Ramsey interferometry of a single probe qubit within a trapped ion experiment. Both methods have the same goal: to measure the work distribution of quantum systems.
Understanding the work distribution of quantum systems could lead to a more comprehensive understanding of quantum thermodynamics, which in turn could lead to some interesting applications.
"A means of measuring the work distribution opens up the possibility of exploring, for the first time, a whole host of thermodynamic phenomena in quantum systems," said Ross Dorner, a PhD student of Professor Vedral and lead author of that paper. "The great thing about our scheme and that of the Belfast team is that they can be adapted to work in a whole range of current experimental technologies, including optical cavities, trapped neutral atoms and potentially many-body systems like Bose-Einstein condensates."
Paternostro added several other potential implications.
"Fundamentally, we could start exploring quantum thermodynamics, which puts together a genuine quantum approach and the rock-solid foundations of thermodynamics," he said. "We (and a few other researchers) are trying to do it from an information theoretic viewpoint, hoping to get new insight into this fascinating area. Practically, the grounding of quantum thermodynamics would imply the incorporation of quantum advantages in thermodynamical processes, such as the engineering of cycles, refrigerators and thermal machines. An example has been provided recently by myself and two colleagues, Dr. Adolfo del Campo (Los Alamos National Lab, US) and Dr. John Goold (University of Oxford and University College Cork, Republic of Ireland), by proposing the scheme for a friction-free quantum Otto machine. In a visionary way, we could build up a thermodynamical machine entirely based on quantum and offering better performances than their classical versions."
Both groups are currently working on experimental implementations of their proposals, which they hope will provide the first clear-cut reconstruction of the work distribution as the basic building block for quantum thermodynamics.
"Our group is working to implement these ideas in the laboratory," Dorner said. "We're also working on theoretical extensions to the idea which might help further improve the accuracy of the measurement scheme and also has applications to the thermometry of many-body quantum systems."
Publication details
R. Dorner, et al. "Extracting QuantumWork Statistics and Fluctuation Theorems by Single-Qubit Interferometry." PRL 110, 230601 (2013). DOI: 10.1103/PhysRevLett.110.230601
L. Mazzola, et al. "Measuring the Characteristic Function of the Work Distribution." PRL 110, 230602 (2013). DOI: 10.1103/PhysRevLett.110.230602
Journal information: Physical Review Letters
© 2013 Phys.org. All rights reserved.