Treegonometry solves Christmas decoration dilemma

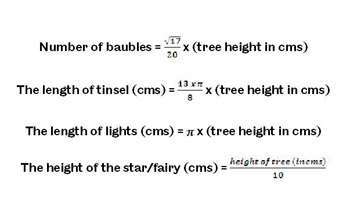
Mathematics has provided an answer for those striving for the perfect Christmas tree, Britain's University of Sheffield says.

The university's Maths Society was set the challenge of decorating a tree so that greenery and glitz are in harmonious proportion, resolving the problem of a tree that is either too barren or gaudy.

Here's their formula:

- Number of baubles: Take the square root of 17, divide it by 20 and multiply it by the height of tree (in centimetres).

- Length of tinsel: 13 multiplied by pi (3.1415) divided by 8, then multiplied by tree height.

- Length of tree lights: Pi multiplied by tree height

- Height (in centimetres) of star or fairy on top of tree: Tree height divided by 10.

"For example, a 180cm (six-feet) Christmas tree would need 37 baubles, around 919 cms of tinsel (30 feet) and 565 cms (19 feet) of lights, and an 18cm (seven-inch) star or angel is required to achieve the perfect look," the University says.

For those seeking an easier way of figuring this out, its website ( www.shef.ac.uk/news/nr/debenha … ree-formula-1.227810 ) has a simple-to-use calculator.

(c) 2012 AFP