June 11, 2012 feature
Proposed experiment would prove that quantum jumps are not objective events
(Phys.org) -- The famous physicist Niels Bohr first conceived of the notion of quantum jumps, or quantum leaps, in 1913. Bohr understood quantum jumps as objective events in which an atom emits or absorbs a photon, causing an electron to jump from one energy level – or quantum state – to another inside the atom. But a few decades later, when physicists began to understand how the act of measuring can affect the result in quantum mechanics, the assumed objectivity of quantum jumps required a second look.
Then in the early 1990s, physicists developed quantum trajectory theory, showing that quantum jumps are not caused by the emission of a photon, but by the detection of a photon. If an emitted photon is not detected, then there is no quantum jump. In other words, quantum jumps are detector-dependent, which is in marked contrast to Bohr’s objective emission events.
Despite the wide acceptance of the assertion that there can be no detector-independent quantum jumps, no experiment has ever been performed to rigorously test this claim.
Now in a new study, physicists Howard M. Wiseman at Griffith University in Queensland, Australia, and Jay M. Gambetta at the IBM T.J. Watson Research Center in Yorktown Heights, New York, have proposed experimental tests to prove that all quantum jumps must be detector-dependent. Their work is published in a recent issue of Physical Review Letters.
“Our work relates to something everyone has heard of (quantum jumps) but says that their fundamental nature has still not been established experimentally,” Wiseman told Phys.org. “By proposing actual experiments, it gives experimentalists a real motivation to try to increase their collection and detection efficiency.”
The proposed tests would rule out not just certain specific detector-independent models of quantum jumps, but all models that could conceivably describe quantum jumps as detector-independent.
As the physicists explain in their study, the key to the tests is to show that there are two different ways to monitor the radiated field of photons emitted by an atom, but the two methods give incompatible results. The procedure is an example of the EPR steering phenomenon, in which two parties (Alice and Bob) share an entangled state. By making measurements (for example, of position and momentum) on her half of the entangled state, Alice can collapse Bob’s half into a different, incompatible state. In this way, Alice shows that Bob’s system does not have an objective quantum state that exists independent of her measurement choice.
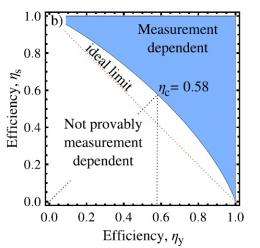
Using similar techniques, the physicists explain how their test can show that two different monitoring techniques give two different results. Mathematically, they show that an EPR steering inequality can be violated when the detector efficiency is above a certain value. Although this efficiency value (0.58) is still very challenging experimentally, achieving it for the new tests would rule out all models – not just the high-efficiency scenarios – that involve detector-independent quantum jumps.
“If the efficiency requirements can be met, then that rules out all models,” Wiseman said. “But if the requirements cannot be met then that doesn't allow us to conclude anything unfortunately. At least, our analysis doesn't imply anything.”
In the future, the physicists hope that these tests will be performed, which would finally prove that quantum jumps are indeed detector-dependent.
“One plan is to try to come up with tests that could be done in systems other than atoms, such as superconducting qubits coupled to a radio-frequency transmission line,” Wiseman said. “We don't yet know what the efficiency requirements would be because the type of dynamics can be quite different. But experimental colleagues (e.g., at Berkeley) in that area are working hard to increase their efficiency anyway.”
More information: Howard M. Wiseman and Jay M. Gambetta. “Are Dynamical Quantum Jumps Detector Dependent?” PRL 108, 220402 (2012). DOI: 10.1103/PhysRevLett.108.220402
Journal information: Physical Review Letters
Copyright 2012 Phys.Org
All rights reserved. This material may not be published, broadcast, rewritten or redistributed in whole or part without the express written permission of PhysOrg.com.