Scientists from the University of Vienna's Faculty of Physics in Austria recently gave a theoretical description of teleportation phenomena in sub-atomic scale physical systems, in a publication in the European Physical Journal D.
For the first time, the Austrian team proved that mathematical tools give us the freedom to choose how to separate out the constituting matter of a complex physical system by selectively analysing its so-called quantum state. That is the state in which the system is found when performing measurement, which can either be entangled or not.
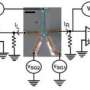
The state of entanglement corresponds to a complex physical system in a definite (pure) state, while its parts taken individually are not. This concept of entanglement used in quantum information theory applies when measurement in laboratory A (called Alice) depends on the definite measurement in laboratory B (called Bob), as both measurements are correlated. This phenomenon cannot be observed in larger-scale physical systems.
The findings of the Austrian team show that the entanglement or separability of a quantum state –whether its sub-states are separable or not; i.e., whether Alice and Bob were able to find independent measurements – depends on the perspective used to assess its status.
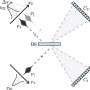
A so-called density matrix is used to mathematically describe a quantum state. To assess this state's status, the matrix can be factorised in different ways, similar to the many ways a cake can be cut. The Vienna physicists have shown that by choosing a particular factorisation, it may lead to entanglement or separability; this can, however, only be done theoretically, as experimentally the factorisation is fixed by experimental conditions.
These findings were applied in the paper to model physical systems of quantum information including the theoretical study of teleportation, which consists of the transportation of a single quantum state. Other practical applications include gaining a better understanding of K-meson creation and decay in particle physics, and of the quantum Hall effect, where electric conductivity takes quantisized values.
Explore further:
Lab sets a new record for creating heralded photons
More information: Entanglement or separability: the choice of how to factorize the algebra of a density matrix W. Thirring et al., European Physical Journal D (2011), DOI: 10.1140/epjd/e2011-20452-1
