March 1, 2011 feature
Time travel experiment demonstrates how to avoid the grandfather paradox (Update)
(PhysOrg.com) -- Among the many intriguing concepts in Einstein’s relativity theories is the idea of closed timelike curves (CTCs), which are paths in spacetime that return to their starting points. As such, CTCs offer the possibility of traveling back in time. But, as many science fiction films have addressed, time travel is full of potential paradoxes. Perhaps the most notable of these is the grandfather paradox, in which a time traveler goes back in time and kills her grandfather, preventing her own birth.
In a new study, a team of researchers has proposed a new theory of CTCs that can resolve the grandfather paradox, and they also perform an experiment showing how such a scheme works. The researchers, led by Seth Lloyd from MIT, along with scientists from the Scuola Normale Superiore in Pisa, Italy; the University of Pavia in Pavia, Italy; the Tokyo Institute of Technology; and the University of Toronto, have published their study in a recent issue of Physical Review Letters. The concepts in the study are similar to an earlier study by some of the same authors that was posted at arXiv.org last year.
“Einstein's theory of general relativity supports closed timelike curves,” Lloyd told PhysOrg.com. “For decades researchers have argued over how to treat such objects quantum mechanically. We believe that our theory is the correct theory of such objects. Moreover, our theory shows how time travel might be accomplished even in the absence of general relativistic closed timelike curves.”
In the new theory, CTCs are required to behave like ideal quantum channels of the sort involved in teleportation. In this theory, self-consistent CTCs (those that don’t result in paradoxes) are postselected, and are called “P-CTCs.” As the scientists explain, this theory differs from the widely accepted quantum theory of CTCs proposed by physicist David Deutsch, in which a time traveler maintains self-consistency by traveling back into a different past than the one she remembers. In the P-CTC formulation, time travelers must travel to the past they remember.
Although postselecting CTCs may seem complicated, it can actually be investigated experimentally in laboratory simulations. By sending a “living” qubit (i.e., a bit in the state 1) a few billionths of a second back in time to try to “kill” its former self (i.e., flip to the state 0), the scientists show that only photons that don’t kill themselves can make the journey.
“P-CTCs work by projecting out part of the quantum state,” Lloyd said. “Another way of thinking about closed timelike curves is the following. In normal physics (i.e., without closed timelike curves), one specifies the state of a system in the past, and the laws of physics then tell how that state evolves in the future. In the presence of CTCs, this prescription breaks down: the state in the past plus the laws of physics no longer suffice to specify the state in the future. In addition, one has to supply final conditions as well as initial conditions. In our case, these final conditions specify the state when it enters the closed timelike curve in the future. These final conditions are what project out part of the quantum state as described above.
“Although one would need a real general relativistic CTC actually to impose final conditions, we can still simulate how such a CTC would work by setting up the initial condition, letting the system evolve, and then making a measurement. One of the possible outcomes of the measurement corresponds to the final condition that we would like to impose. Whenever that outcome occurs, then everything that has happened in the experiment up to that point is exactly the same as if the photon had gone backward in time and tried to kill its former self. So when we ‘post-select’ that outcome, the experiment is equivalent to a real CTC.”
To demonstrate, the scientists stored two qubits in a single photon, one of which represents the forward-traveling qubit, and one of which represents the backward-traveling qubit. The backward-traveling qubit can teleport through a quantum channel (CTC) only if the CTC ends by projecting the two entangled qubits into the same state.
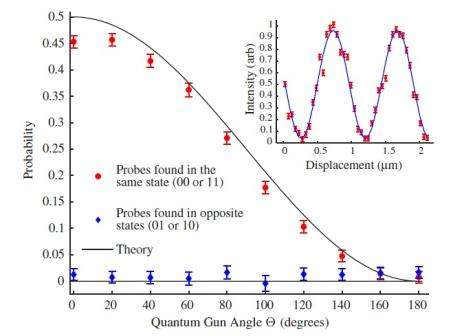
After the qubits are entangled, their states are measured by two probe qubits. Next, a “quantum gun” is fired at the forward-traveling qubit, which, depending on the gun’s angle, may or may not rotate the qubit’s polarization. The qubits’ states are measured again to find out if the gun has flipped the forward-traveling qubit’s polarization or not. If both qubits are in the same state (00 or 11), then the gun has not flipped the polarization and the photon “survives.” If the qubits’ states are not equal (01 or 10), then the photon has “killed” its past self. The experiment’s results showed that the qubits’ states were almost always equal, showing that a qubit cannot kill its former self.
The scientists noted that their experiment cannot test whether an actual CTC obeys their new theory, since it is currently unknown whether CTCs exist at all. In the future, they plan to perform more tests to better understand time travel paradoxes.
“We want to perform the so-called `unproved theorem paradox' experiment, in which the time traveler sees an elegant proof of a theorem in a book,” Lloyd said. “She goes back in time and shows the proof to a mathematician, who includes the proof in the book that he is writing. Of course, the book is the same book from which the time traveler took the proof in the first place. Where did the proof come from? Our theory has a specific prediction/retrodiction for this paradox, which we wish to test experimentally.”
More information: Seth Lloyd, et al. “Closed Timelike Curves via Postselection: Theory and Experimental Test of Consistency.” Physical Review Letters 106, 040403 (2011). DOI:10.1103/PhysRevLett.106.040403
Copyright 2010 PhysOrg.com.
All rights reserved. This material may not be published, broadcast, rewritten or redistributed in whole or part without the express written permission of PhysOrg.com.