Strange new twist: Researchers discover Mobius symmetry in metamaterials

Xiang Zhang, a scientist with the U.S. Department of Energy's Lawrence Berkeley National Laboratory (Berkeley Lab) and a professor at the University of California (UC) Berkeley, led a study in which electromagnetic Möbius symmetry was successfully introduced into composite metamolecular systems made from metals and dielectrics. This discovery opens the door to finding and exploiting novel phenomena in metamaterials.

"We have experimentally observed a new topological symmetry in electromagnetic metamaterial systems that is
equivalent to the structural symmetry of a Möbius strip, with the number of twists controlled by sign changes in the electromagnetic coupling between the meta-atoms," Zhang says. "We have further demonstrated that metamaterials with different coupling signs exhibit resonance frequencies that depend on the number but not the locations of the twists. This confirms the topological nature of the symmetry."

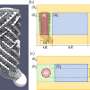
Working with metallic resonant meta-atoms configured as coupled split-ring resonators, Zhang and members of his research group assembled three of these meta-atoms into trimers. Through careful design of the electromagnetic couplings between the constituent meta-atoms, these trimers displayed Möbius C3 symmetry – meaning Möbius cyclic symmetry through three rotations of 120 degrees. The Möbius twists result from a change in the signs of the electromagnetic coupling constants between the constituent meta-atoms.

"The topological Möbius symmetry we found in our meta-molecule trimers is a new symmetry not found in naturally occurring materials or molecules." Zhang says. "Since the coupling constants of metamolecules can be arbitrarily varied from positive to negative without any constraints, the number of Möbius twists we can introduce are unlimited. This means that topological structures that have thus far been limited to mathematical imagination can now be realized using metamolecules of different designs."

Details on this discovery have been published in the journal Physical Review Letters, in a paper titled "Optical Möbius Symmetry in Metamaterials." Co-authoring the paper with Zhang were Chih-Wei Chang, Ming Liu, Sunghyun Nam, Shuang Zhang, Yongmin Liu and Guy Bartal.

Xiang Zhang is a principal investigator with Berkeley Lab's Materials Sciences Division and the Ernest S. Kuh Endowed Chaired Professor at UC Berkeley, where he directs the Center for Scalable and Integrated NanoManufacturing (SINAM), a National Science Foundation Nano-scale Science and Engineering Center.

Enlarge

In his “parade of ants,” Artist M.C. Escher demonstrated that it is possible to traverse the “inside” and “outside” surfaces of a Möbius band without crossing over an edge.

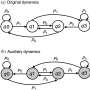
While some symmetries, such as spatial geometries, are easily observed, others, such as optical symmetries, may be hidden. A powerful investigative tool for uncovering hidden symmetries is a general phenomenon known as "degeneracy." For example, the energy level degeneracy of an atom in a crystal is correlated with the crystal symmetry. A three-body system, like a trimer, can be especially effective for studying the correlation between degeneracy and symmetry because, although it is a relatively simple system, it reveals a rich spectrum of phenomena.

"The unique properties of a three-body system make experimental investigations of hidden symmetries possible," says Chih-Wei Chang, a former post-doc in Zhang's group and the lead author of the paper in Physical Review Letters, says. "Intrigued by the extraordinary engineering flexibilities of metamaterials, we decided to investigate some non-trivial symmetries hidden beneath these metamolecules by studying their degeneracy properties"

The authors tested their metamaterials for hidden symmetry by shining a light and monitoring the optical resonances. The resulting resonant frequencies revealed that degeneracy is kept even when the coupling constants between meta-atoms flip signs.

"Because degeneracy and symmetry are always correlated, there must be some symmetry hidden beneath the observed degeneracy" says Chang.

The researchers showed that whereas trimer systems with uniform negative (or positive) coupling signs could be symbolized as an equilateral triangle, trimer systems with mixed signs of couplings could only be symbolized as a Möbius strip with topological C3 symmetry. Furthermore, in other metamolecular systems made of six meta-atoms, the authors demonstrated up to three Möbius twists.

Says Chang, now a faculty member at National Taiwan University in Taipei, "When going from natural systems to artificial meta-atoms and metamolecules, we can expect to encounter phenomena far beyond our conventional conceptions. The new symmetries we find in metamaterials could be extended to other kinds of artificial systems, such as Josephson junctions, that will open new avenues for novel phenomena in quantum electronics and quantum optics."

Provided by Lawrence Berkeley National Laboratory