Breakthrough in light manipulation: Unveiling novel finite barrier bound states

Exploring wave propagation and localization in various media has been a core focus in optics and acoustics. Specifically, in photonics and phononics, scientists have been dedicated to understanding and controlling the behavior of light and sound waves in periodic media.

With their unique bandgap properties, photonic crystals offer an excellent platform for studying wave propagation and localization. These bandgaps, caused by the periodic structure of the crystal, can control wave propagation and even completely inhibit waves in certain frequency ranges.

Traditionally, it was believed that boundary modes in photonic crystals are strongly influenced by the size of the crystal (number of lattice sites). It was generally assumed that these modes are more easily confined in large systems (with many lattice sites) as the probability of tunneling decreases significantly with increasing system size. This phenomenon is critical in designing and implementing high-performance photonic devices, particularly in pursuing high integration and miniaturization of devices.

Additionally, in photonic crystal research, bound states in the continuum (BICs) have attracted attention as they reveal that certain unique modes can be confined within specific regions even in the continuous spectrum. This phenomenon provides a new perspective for understanding and controlling the localization of light waves. It shows great potential in practical applications, such as improving the performance and efficiency of optical devices.

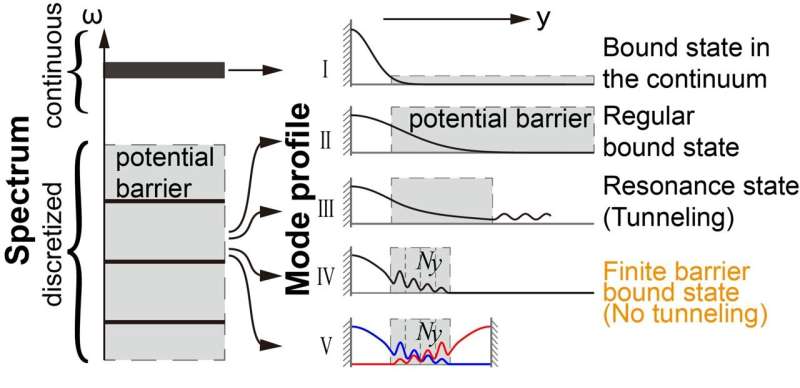
New research published in Light: Science & Applications proposes and confirms the existence of finite barrier bound states. The spectrum of a system typically consists of continuous and discrete spectra (left panel of Fig. 1). Conventional wisdom holds that the eigenvalue spectrum of bound states is discrete, while unbound states form a continuous spectrum.

For instance, in electronic systems, if the particle's energy is lower than the potential energy at infinity, the state is bound with a discrete spectrum; whereas particles with energy higher than the potential energy scatter, forming a continuous spectrum.

For light and sound waves, discrete states form due to boundary conditions imposed by a barrier, such as a "bandgap." These discrete states can be localized entirely in ideal conditions (infinite barrier width, Fig. 1-II). However, when the barrier width is finite, there's a probability for the state to tunnel through the barrier and become a resonant state (Fig. 1-III).

Notably, bound states in the continuum (BICs) are spatially bound within the continuous spectrum's energy/frequency range (Fig. 1-I). This study introduces a counterintuitive concept parallel to BICs: certain states can be bound entirely in very thin bandgap materials, making them unable to tunnel through the bandgap material (Fig. 1-IV and 1-V).

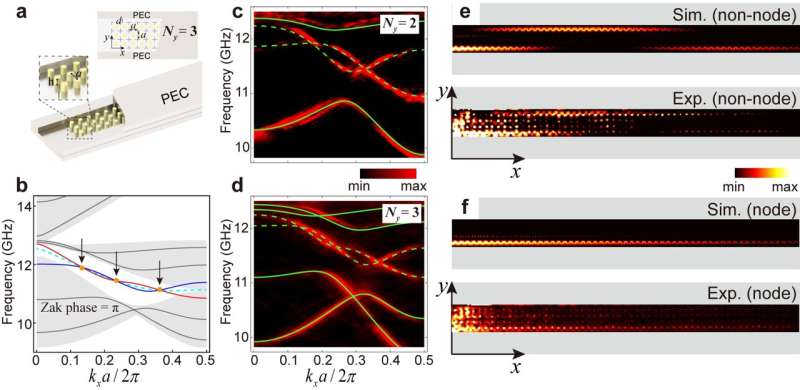
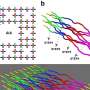
The study first demonstrates a special mirror-symmetric photonic crystal strip structure where the transition of boundary modes can be finely controlled. When the width of the photonic crystal (the number of lattice sites along the y-direction, N_y) is small, the boundary modes on both sides interact and split into odd and even modes (Fig. 2 a–d).

At specific wave vectors (nodes), the coupling strength of the boundary modes is zero. Even if the width (N_y) of the photonic crystal is very small, the boundary mode cannot jump from one side of the photonic crystal to the other (Fig. 2 e–f). Generally, it is believed that many lattice sites are required to suppress the coupling of boundary modes. Still, this study challenges this view and opens a new method for manipulating photon behavior at the microscopic scale.

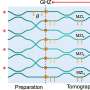
Following the previous configuration, researchers remove one PEC boundary of the photonic crystal, revealing a new configuration. They discovered that the remaining boundary modes at specific nodal wave vectors are entirely trapped, forming Finite Barrier Enabled Bound States in the Continuum (FBICs).

These FBICs exhibit non-radiating properties due to the decoupling of the two boundary modes. At the nodes, where the coupling strength of boundary modes is zero, a state with a radiation coefficient of zero exists when one side of the PEC is removed, and its frequency matches the nodal frequency found in the double PEC scenario, identifying it as an FBIC.

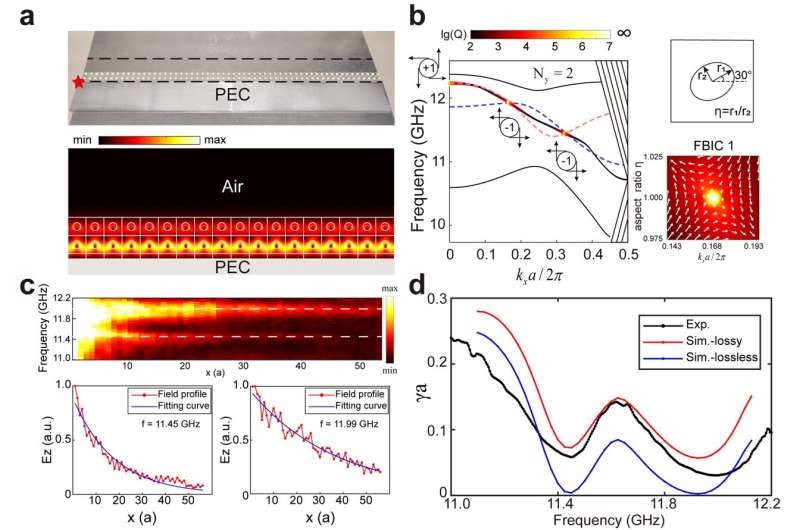
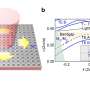
Additionally, by altering the circular dielectric to elliptical to break the original mirror symmetry and introducing a new geometric parameter η, the study defined a winding number in the kx-η parameter space, revealing the topological characteristics of FBICs and confirming these modes as BICs (Fig. 3 a–b).

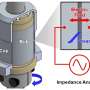
Considering the unavoidable dielectric loss at microwave frequencies, the study experimentally validated FBICs by measuring the attenuation of boundary modes (Fig. 3 c–d), demonstrating complete localization of boundary modes within very few lattice sites (N_y=2, 3, etc.), offering a novel approach to achieve BICs.

This groundbreaking study explores novel physical phenomena in photonic crystals and achieves fine control of boundary modes. This work not only provides a new understanding of the tunneling and bounding of boundary modes in photonic crystals theoretically but also confirms the complete localization of boundary modes at specific wave vectors through microwave experiments, bringing a new perspective to the field of photonics.

The research reveals new methods for manipulating photon behavior, which is significant for developing highly integrated photonic devices. It also offers new strategies for using photonic crystals to enhance light-matter interactions, potentially leading to breakthroughs in nonlinear optics and interactions between light and two-dimensional materials. These findings may inspire future research, such as applying these principles to other wave systems like phononic crystals.