Vectorial spin-orbital Hall effect of light upon tight focusing and experimental observation in azopolymer films

A soccer player can kick a static ball on its side, forcing the ball to rotate and travel in an arc trajectory, left or right curved, depending on the ball's rotation sense. This requires skill/experience. And if the ball is not static but approaches the player already spinning—the control of the ball demands knowledge on how to manipulate/kick it depending on its characteristics and the intended trajectory.

A somewhat similar effect exists in optics, namely spin Hall effect of light (SHEL). Here, the optical beam/the ball is focused/"kicked" by the lens/player on the side/being initially shifted from the optical axis. As a result, the beam is focused not in the center of the focal plane, but with some deviation from it, depending on the light spin (its electric field clockwise or counterclockwise rotation) and vorticity (its phase rotation). Relating the beam properties in the focal plane/football goal to the beam spin and vorticity will allow mastering of the beam/ball hitting the target.

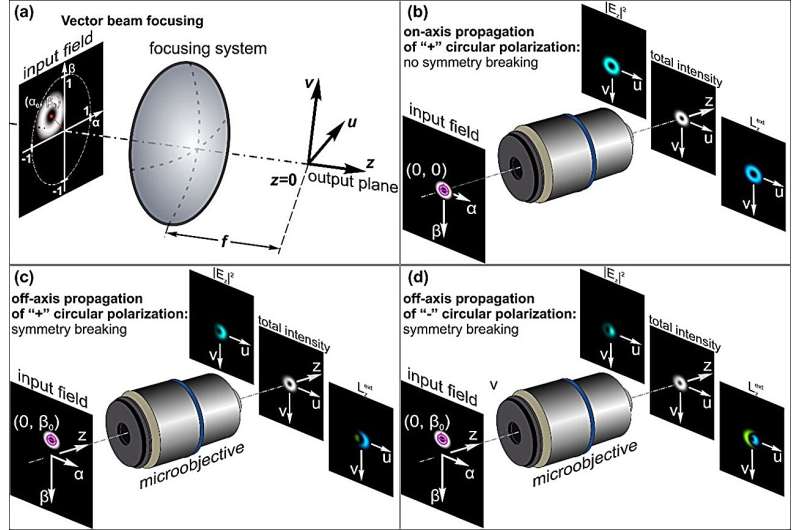
The authors of an article published in Opto-Electronic Science introduce vectorial analysis of spin-orbital Hall effect of light upon tight focusing in free space. This is one of the most prominent effects due to symmetry breaking, in this case (focusing) using an asymmetric incident light beam.

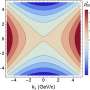
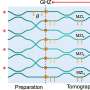
The effect is exhibited as a shift of the focused beam in the transverse focal plane, depending on the sense of spin and orbital angular momentum OAM and the magnitude of OAM, and is the consequence of the requirement to conserve angular momentum (AM). An example of this effect is shown in Figure 1.

Physically, an asymmetric input beam has an external OAM, L^ext∝(r×p), where r is the radius and p is linear momentum. For example, where E_i is an electric field component. Thus, conservation of this momentum at the focus necessitates off-axis shift of the electric field components.

Similar arguments can be invoked in relation to the SAM: the asymmetric input beam after the lens has both transverse and longitudinal SAM components expressed through product of electric field components E_i*E_j, and this also requires corresponding shifts in the electric field distribution in the focal plane. Thus, the light has to "self-organize" or restructure itself in the focus to satisfy angular momentum conservation law.

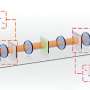
The above deliberations point at the importance of knowing the distribution of different components of the focused asymmetric input beam possessing spin and/or vorticity. Previously, only the shifts of the longitudinal/z component of the field or its total intensity were studied, and this was studied in cylindrical coordinates.

Since, for an asymmetric input beam, the azimuthal symmetry of the system is broken, it makes sense to use Cartesian coordinates, which is exactly the accomplishment of this study. The present work shows, both analytically and by numerical simulation, how different electric field components are displaced upon tight focusing of an asymmetric light beam as a function of OAM and spin.

The main result of the analytical and numerical simulations presented is that upon focusing of an asymmetric beam possessing angular momentum all three Cartesian components of the electric field in the focal plane experience shifts and/or are redistributed. The relation between field components shifts and the AM components shifts/redistribution is shown too. This redistribution of spin and orbital angular momentum is manifested in spin-orbit and orbit-orbit conversions and reorganization, i.e., spin–orbit and orbit–orbit interaction.

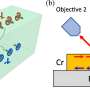
In addition, occurrence of orbit-spin conversion is presented too, when OAM is either directly transformed to SAM and/or acts as catalyzer to redistribution of SAM. Moreover, for the first time, the spin-orbit Hall effect of light upon tight focusing in free space is experimentally demonstrated. This is achieved using azopolymers as a media detecting longitudinal or z component of the electrical field of light. Figure 2 shows one of the experimental results. These findings elucidate the Hall effect of light and may broaden the spectrum of its applications.