This article has been reviewed according to Science X's editorial process and policies. Editors have highlighted the following attributes while ensuring the content's credibility:
fact-checked
trusted source
written by researcher(s)
proofread
How to make better decisions—using scoring systems

When faced with difficult choices, we often rank the alternatives to see how they stack up. This approach is ubiquitous, used from major business and policy decisions, through to personal choices such as the selection of a university course, place to live, or political voting preference.
Typically, criteria are identified and each one is "weighted" according to importance. The options are then scored against each criterion and the weightings applied. But this common approach is frequently flawed and not as rational as it first seems.
Decision-making usually involves choosing from a limited range of options. When there is only one criterion to consider, such as cost, the decision is straightforward. Normally, however, there are pros and cons to balance up for each option. A process known as multi-criteria decision analysis is often used to weigh alternatives in this way.
There are many variants, but the weighted-sum method is the most common. This technique appears superficially simple, logical and intuitive. Typically, the decision-maker starts by eliminating any options that fail to deliver one or more essential requirements, which are termed the "needs".
The second stage involves sorting the remaining options into an order according to preference. This preference order is based on how well the options satisfy the other requirements, which are termed the "wants". The needs must be satisfied, whereas the wants are attributes to maximize. Eliminating options that fail to meet the needs is straightforward, but combining the wants is more complicated.
To evaluate options against the wants, the decision-maker draws up a table in which column headings represent the different alternatives and row headings represent the wants. Scores are placed in the cells of the table to represent the performance of each option against each want. Some wants are more important than others, so each one is given an importance weighting.
Typically, the scores and weightings, or "weights", are both chosen on a scale from zero to ten. Each score is then multiplied by its corresponding weight and additional columns can be inserted in the table for this purpose. The weighted scores are then added together for each option. Finally, the options are ranked according to their total weighted score.
A variant is the weighted-product method, where the weighted scores for each option are multiplied together, rather than added together. It requires all values to be at least one. This method favors good all-round performance, whereas the weighted-sum method is more forgiving of wide variations in performance.
Flaws in the conventional approach
A weakness in most of these multi-criteria decision analyzes is their dependence on number values to express ideas that depend on a human evaluation—in other words, they are "qualitative".
Aside from those difficulties, the straightforward multiplication of a score by an importance weighting has inherent pitfalls if a simple scale like zero to ten is used. Where a want is considered important—has a high importance weighting—and a candidate performs well with respect to that want, the weighted score will be high, as expected.
Where a want is considered less important and an option performs poorly with respect to that want, the method will give that option a low-weighted score. However, since the want in question has a low importance weighting, the option should not be penalized harshly and should remain in contention.
Ideally, the lowest weighted scores ought to be those ascribed to options with a low score against a highly weighted want. They should not be given to options that score low against a want that has a low weighting and is therefore inconsequential. So, although the standard approach works for identifying the best options, it is poor at ranking the alternatives and it gives a false impression of the worst options.
Consider such an approach being used to allocate funding, based on applications for a grant. Rival bids might be scored against wants such as innovation, quality, timeliness and value-for-money, each of which is weighted according to importance. The smallest awards ought to be given to the bids with the lowest scores against the most important criteria. Instead, the bids ranked bottom are those with low scores against criteria that are least important.
A better approach
These problems can be addressed by using a scoring scale that includes negative values. The alternative inference mechanism (AIM) method, makes the necessary adjustments while keeping an intuitive range of scores, such as zero to ten.
AIM recognizes that the worst candidates are those with low scores against wants that have high importance weightings. On the other hand, candidates that score poorly against an unimportant want are not severely disadvantaged.
The chart below contrasts AIM with the conventional approach. The two methods agree on the best options, which are the green ones clustered at the top-right. However, the worst options in red or orange are at the bottom-left using the conventional approach, and at the bottom-right with AIM.
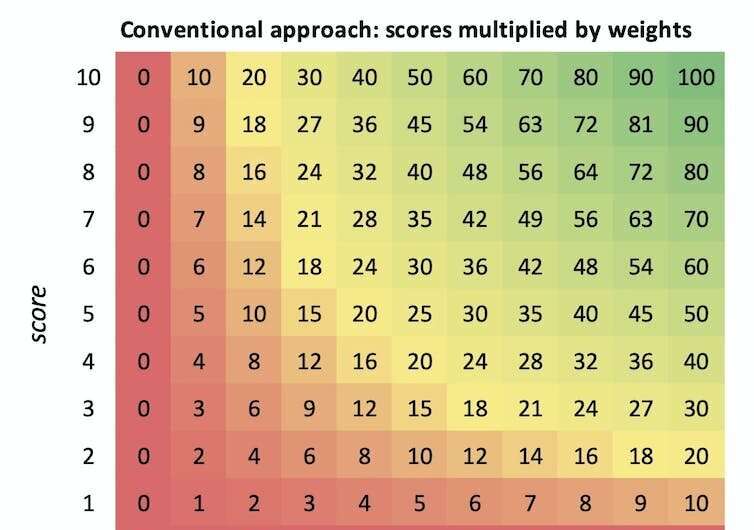
The conventional approach has a row of zeros across the bottom, as it ranks candidates equally if they score zero against a want, regardless of its importance. Similarly, it has a column of zeros up the left side, as it penalizes all candidates against unimportant criteria, regardless of their score. In contrast, AIM has a lot of yellow on the left side, indicating that unimportant scores are neither good nor bad—a much more logical and a rational basis for sound decision-making.
Multi-criteria decision analysis can be an excellent tool for choosing between alternative options, but understanding the weighting mechanism is vital.
AIM was previously described in a specialized engineering journal, but its wider appreciation and adoption could improve decision-making across society. The conventional scoring model has only persisted though an unquestioning acceptance of its validity.
AIM has shown the value of probing a little deeper into the meaning of the numbers. With greater awareness of rational models like AIM, we could make better decisions in all aspects of our lives.
Provided by The Conversation
This article is republished from The Conversation under a Creative Commons license. Read the original article.![]()