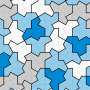
Close relative of aperiodic tile 'the hat' found to be a true chiral aperiodic monotile

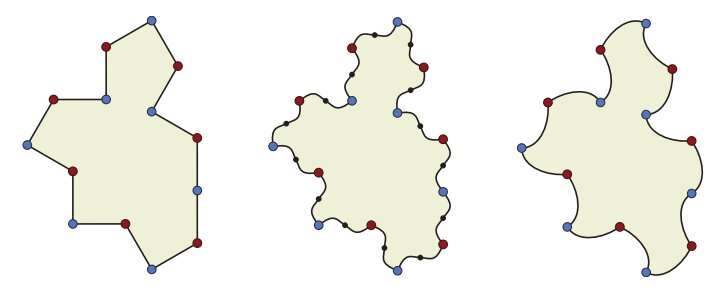
Mathematicians from Yorkshire University, the University of Cambridge, the University of Waterloo and the University of Arkansas have one-upped themselves by finding a close relative of "the hat," a unique geometric shape that does not repeat itself when tiled, that is a true chiral aperiodic monotile. David Smith, Joseph Samuel Myers, Craig Kaplan and Chaim Goodman-Strauss have published a paper outlining their new find on the arXiv preprint server.

Just three months ago, the same four mathematicians announced what has come to be known in the field as the "einstein" shape—a single shape that could be used for aperiodic tiling all by itself. They called it "the hat."

The finding appeared to be the final step in the 60-year search for such a shape. Prior efforts had led to multi-tile results that had been whittled down to just two as recently as the mid-1970s. But since that time, efforts to find the einstein shape failed—until this past March, when the team on this new effort made their announcement.

But others in the field pointed out that the shape described by the team was not, technically, a single aperiodic tile—it and its mirror image are two unique tiles and both are needed to create the shape described by the team. Apparently agreeing with the assessment of their colleagues, the four mathematicians took another look at their shape and found that by slightly modifying it, the need for its mirror would no longer exist and it indeed represented the true einstein shape.

Notably, the name used to describe the shape is not a nod to the famous physicist—it comes from a German phrase meant to denote "one stone." The team refers to the new shape simply as a close relative of the hat. They also note that they found that modifying the edges of the newly discovered polygon in certain ways creates a whole family of shapes, called Spectres—all strictly chiral aperiodic monotiles.

© 2023 Science X Network