Mathematicians propose alternative method to map neuron activity
A paper by researchers in the University at Buffalo's Department of Mathematics that could impact the way neuron-to-neuron communications are mapped was recently published in Communications Physics.
The paper, titled "Simplicial cascades are orchestrated by the multidimensional geometry of neuronal complexes," was authored by Dane Taylor, Ph.D., assistant professor of mathematics, and UB Ph.D. candidate Bengier Ulgen Kilic. It discusses new methods for the mathematical modeling of neuronal networks. The paper appeared in the Nov. 8 issue of the journal.
The main goal of the research is to better understand the biological and mathematical mechanisms that allow brains to manifest memories as neuron activity patterns that can be stored and reliably called upon later for cognitive processing, Taylor said.
Kilic said the work will "lay the pavement for integrating rapidly growing in vivo experimental data with theoretical frameworks, particularly in artificial intelligence and computational neuroscience domains."
In general, higher-order communication is a hard concept to grasp in the context of the brain network, Kilic said. "However, we know that nervous systems are balls of neurons, and every single neuron in our nervous system is bombarded with synaptic signals at any second.
"Although the manner in which neurons communicate remains a mystery, there is evidence that behavior that lies beneath human cognition and consciousness in part emerges from these higher-order interactions," Kilic said.
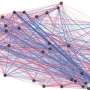
In their paper, Taylor and Kilic study the speed and rate of dissemination of neuronal activity using the "mathematical" lens of geometry and topology.
The process of modeling neurons—those cells that transmit information throughout the brain and nervous system via electrical impulses—involves representing the neuron's biophysical and geometrical characteristics with a mathematical structure, such as a graph.
Neuronal networks are believed to encode memory using nonlinear functions that translate a set of inputs—the activities of neurons that influence another neuron—into a neuron response, Taylor said. "Different input patterns give rise to different neuron responses, and a graph-based model is an oversimplification for the possible types of responses."
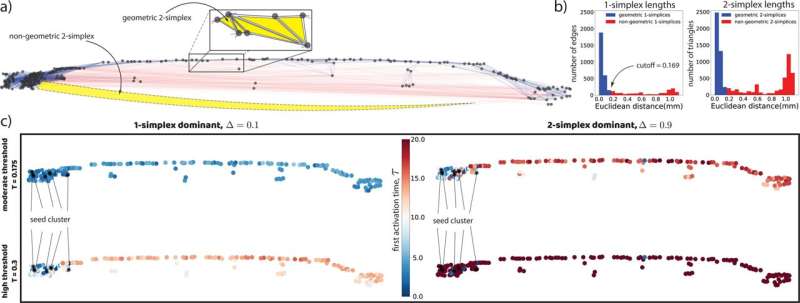
Taylor and Kilic propose expanding these graphs into simplicial complexes—or hypergraphs—that can map connections between vast networks of neurons.
"Historically, the modeling and analysis of both biological neuronal networks and synthetic neuronal networks (for AI) have relied on building models that are based on the mathematical framework of two-dimensional graphs," Taylor said.
"This is, in part, due to the added mathematical complexity that arises when trying to keep track of dyadic, triadic, and higher-order interactions among groups of neurons," he said.
"For example, the activity of three neurons that jointly interact through a three-way relationship, can be significantly more complicated than that for three neurons whose interactions are limited to two-way relationships between pairs of neurons," he said.
"The firing of several nearby neurons can lead to an avalanching cascade of neuron firings that spreads across a neuronal network," Taylor said. "Such neuronal avalanches have been widely observed and have been empirically connected to memory formation and cognitive function, such as human logic and intuition."
Taylor used the following analogy to illustrate the difference between traditional models and simplicial models.
"Consider if your friends and family and coworkers all give you different information and recommendations about whether or not to go see a newly released movie. A simplicial complex model, or equivalently, a hypergraph model, would allow you to make a decision by incorporating all the information provided by everyone in a complicated, unconstrained way," he said.
"In contrast, a graph-based model for your ultimate decision would involve you considering each person's recommendation independently, making a separate initial decision for each recommendation. Given a set of initial decisions, you combine them to make your ultimate decision," he said. "Thus, your final decision is made based on initial, independent sub decisions, rather than making a fully informed decision that integrates all the available information together from everyone."
Taylor said it well-known that neuron activity spreads as a cascade of spiking activity, which he likened to epidemic spreading and cascading blackouts in a power grid. But very little is known about the neuronal mechanisms that can guide the cascades of spiking neurons.
"We leveraged advanced mathematical modeling to identify a plausible mechanism that can orchestrate such cascades, and the next step will be to team up with neuroscientists that can experimentally test our hypothesized mechanism," he said.
For Taylor and Kilic, its application for AI is a longer-term goal, although other students in his group are studying it. Taylor said it will be up to two years before they redirect the current project from studying biological neurons to artificial neural networks.
More information: Bengier Ülgen Kilic et al, Simplicial cascades are orchestrated by the multidimensional geometry of neuronal complexes, Communications Physics (2022). DOI: 10.1038/s42005-022-01062-3
Journal information: Communications Physics
Provided by University at Buffalo