Generalizing the measurement postulate in quantum mechanics
The measurement postulate is crucial to quantum mechanics. If we measure a quantum system, we can only get one of the eigenvalues of the measured observable, such as position, energy and so on, with a probability. Immediately after the measurement, the system will collapse into the corresponding eigenstate instantly, known as state collapse. It is argued that the non-cloning theorem is actually a result of the measurement postulate, because non-cloning theorem would also hold in classical physics. The possibility of cloning in classical physics is actually the ability to fully measure a classical system, so that a classical state can be measured and prepared.
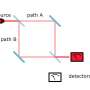
To explain clearly the measurement in quantum mechanics, it is better to use the following example. Suppose a photon passes through a three-identical-slits and we place an ideal and nondemolition detector after each of the slit. According to the measurement-postulate, one of the detectors will detect the photon, and as a result the whole wavefunction will collapse into that slit.
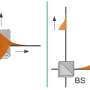
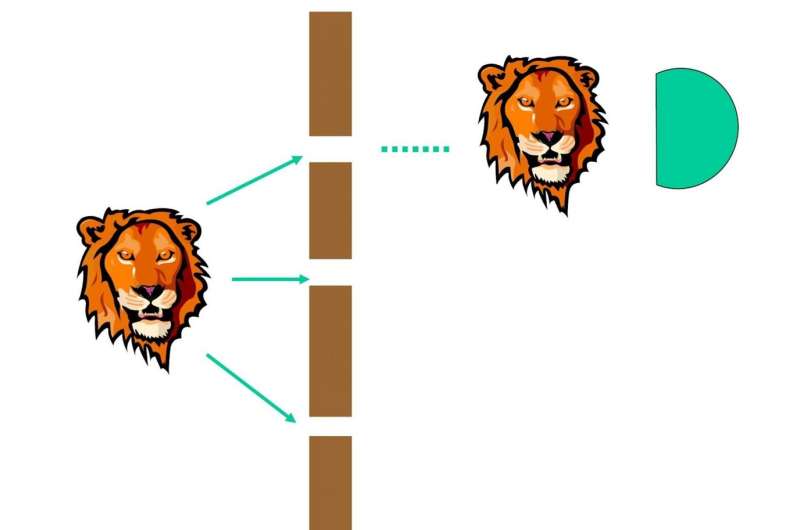
What will happen if we just place only a single detector after the upper slit? It is natural to think that it will have one third probability to detect the photon, and collapses the whole wavefunction into slit-1, as shown in Fig. 2. However, what will happen if the detector at upper slit does not measure the photon? This is a partial measurement. This was encountered in the duality quantum computing formalism, where linear combination of unitaries (LCU) was proposed to perform quantum computing.
Long proposed that when measuring a partial wave, something will surely happen: (1) collapse-in: it will collapse into one of the eigenvalues with some probability. After the measurement, the whole wavefunction will change instantly to the corresponding eigenstate; (2) collapse-out: the measured wavefunction will disappear, and shift to the unmeasured part. As shown in Fig. 2, the detector will measure the photon with probability 1/3, and the whole photon wavefunction collapses into the upper slit. As shown in Fig. 3 for collapse-out, the measured part in the upper slit disappears, and the unmeasured part, namely the wavefunction in the middle-slit and lower-slit increases.
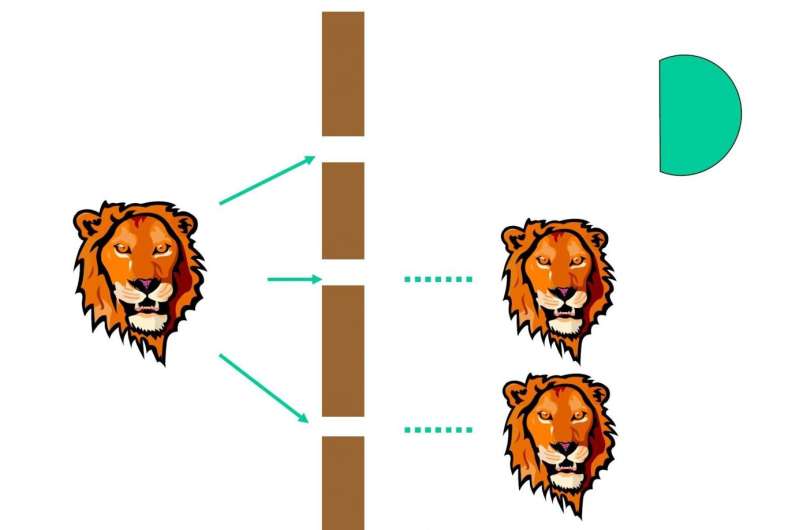
In reality, partial measurement is more common than full measurement. It should be noted that collapse-in and collapse-out of partial measurement happens randomly not only in space, but also over time. For instance, the detection of photon by a detector can be naturally understood in terms of this partial measurement postulate. When the wavefunction of a photon goes to a detector, it is not measured in full at the same time, namely it is not a full measurement. Its front part arrives at the detector first, hitting some area of the detector. It either collapses in at any point of the intersecting area in the detector or collapses and the corresponding probability will be shifted to other part of the wavefunction. This process continues until the photon is detected. If the photon has not been detected until the last part of the wavefunction reaches the detector, then the amplitude of this remaining wavefunction increases to 1 so as to detect the photon with certainty at the final step.
This explanation is given in the view that Wavefunction Is just the quantum system Entity itself, the WISE interpretation. In WISE interpretation, there is NO relation between the wavefunction and the quantum system, the wavefunction IS just the quantum system. The WISE interpretation is supported by the encounter delayed choice experiment, which has been reported in various media a few years ago.
More information: GuiLu Long, Collapse-in and collapse-out in partial measurement in quantum mechanics and its wise interpretation, Science China Physics, Mechanics & Astronomy (2021). DOI: 10.1007/s11433-021-1716-y
Provided by Science China Press