When physics meets financial networks

Generally, physics and financial systems are not easily associated in people's minds. Yet, principles and techniques originating from physics can be very effective in describing the processes taking place on financial markets. Modeling financial systems as networks can greatly enhance our understanding of phenomena that are relevant not only to researchers in economics and other disciplines, but also to ordinary citizens, public agencies and governments. The theory of Complex Networks represents a powerful framework for studying how shocks propagate in financial systems, identifying early-warning signals of forthcoming crises, and reconstructing hidden linkages in interbank systems.
In a review article appearing on Nature Reviews Physics, several scholars in Complex Networks have now teamed up to organize and update the knowledge in the field. The article summarizes over 15 years of truly interdisciplinary research, highlighting how the statistical physics approach has shed light on various key properties of these phenomena. The authors represent some of the most internationally active research groups in the field, based at the IMT School for Advanced Studies Lucca, the University of Leiden, Ca' Foscari University of Venice, University of Zurich, Tor Vergata University of Rome, University College London and the Bank of England.
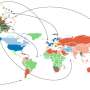
The starting point of the analysis is the recognition that financial institutions are linked together in a global web of interactions whose structure can be analyzed quantitatively by means of network theory, the framework that studies the structure and consequences of the relationships connecting different objects in large systems. In fact, the financial system can be viewed as a network whose nodes represent agents—e.g. retail and investment banks, insurance companies, investment funds, central banks but also non-financial firms and households—and whose edges represent dependencies between nodes.
The models traditionally employed by regulators and policymakers consider far too simple representations of financial systems, describing them either as collections of isolated actors or as a homogeneous "mixture" where each actor interacts equally with all the other ones. However, as the 2007-2008 crisis showed dramatically, both representations fail to provide an appropriate description of the highly heterogeneous and intertwined structure of these systems, as well as the implications for society. When the crisis struck, banks that broke down could not repay their debt, causing other banks to go bankrupt, in a cascading effect whose dynamics strongly depended on the details of the interconnection patterns. Policymakers admitted that they felt abandoned by traditional economic models.
Here is where network theory comes into play, by clarifying the interplay between the structure of the network, the heterogeneity of the individual characteristics of financial actors and the dynamics of risk propagation, in particular contagion, i.e. the domino effect by which the instability of some financial institutions can reverberate to other institutions to which they are connected. The associated risk is indeed "systemic", i.e. both produced and faced by the system as a whole, as in collective phenomena studied in physics. "Each bank determines the interest rate for loans to other banks based on their perceived individual riskiness," explains Diego Garlaschelli, Associate Professor at the IMT School for Advanced Studies Lucca and at Leiden University, the Netherlands. "However if those banks are in turn interconnected via other loans, then the actual risk of a collective default can be much higher. Since the existence of loans is a matter of confidentiality, one has to devise new techniques to guess the key properties of interbank networks from partial information. This is crucial also for central banks that strive to run reliable stress tests on the financial system. A nontrivial generalization of the statistical physics framework allowed us to address this challenge in an original way."
The publication in Nature Reviews Physics is a recognition of the fact that financial networks are one of the new frontiers of modern physics; besides, it acknowledges the key role played by statistical physics in providing a mathematical description of the relation between microscopic and macroscopic properties of systems composed of many parts, including social and economic ones.
The authors of the review have been working in the field of financial networks for several years. "Our network reconstruction methods have been tested by various groups worldwide, including one uniting researchers from several central banks, and have been found to systematically outperform the alternative ones," says Tiziano Squartini, Assistant Professor in physics at the IMT School. "In collaboration with the Dutch Central Bank, we even found that, while the 2007-2008 crisis came as a surprise to traditional models, a network analysis accounting for the observed heterogeneity of banks could have predicted it three years in advance."
Today, after almost fifteen years from the financial crisis, the role of networks for monitoring financial stability and designing macroprudential regulation is widely recognized. Both policymakers and researchers agree that systemic risk has to be studied and managed by adopting a network perspective. Besides, it is necessary that institutions adopt network models for risk assessment more comprehensively. This is also reflected in the policy action and discourse of the highest financial authorities, both in the US and in the EU.
More information: Marco Bardoscia et al, The physics of financial networks, Nature Reviews Physics (2021). DOI: 10.1038/s42254-021-00322-5
Provided by IMT School for Advanced Studies Lucca