New physical picture leads to a precise finite-size scaling of (3+1)-dimensional O(n) critical system
Since the establishment of the renormalization group theory, it has been known that systems of critical phenomena typically possess an upper critical dimension dc (dc=4 for the O(n) model), such that in spatial dimensions at or higher than the dc, the thermodynamic behavior is governed by critical exponents taking mean-field values. In contrast to the simplicity of the thermodynamic behavior, the theory of finite-size scaling (FSS) for the d>dc O(n) model was surprisingly subtle and had remained the subject of ongoing debate till recently, when a two-length scaling ansatz for the two-point correlation function was conjectured, numerically confirmed, and partly supported by analytical calculations.
At the upper critical dimensionality dc, multiplicative and additive logarithmic corrections generally occur to the bare mean-field behavior. The clarification of logarithmic corrections in FSS becomes 'notoriously hard,' due to the lack of analytical insights beyond the phenomenological level and the limit of system sizes available in numerical simulations. The precise logarithmic FSS form at d=dc has remained a long-standing problem.
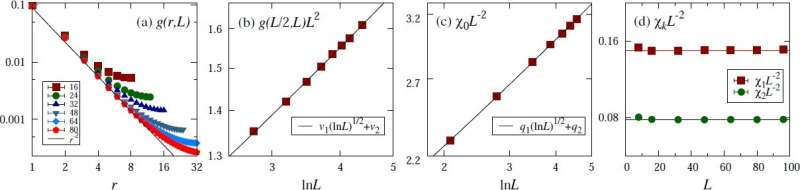
Recently, Jian-Ping Lv, Wanwan Xu, and Yanan Sun from Anhui Normal University, Kun Chen from Rutgers, the State University of New Jersey, and Youjin Deng from University of Science and Technology of China and Minjiang University addressed the logarithmic FSS of the O(n) symmetry at the upper critical dimensionality. Borrowing insights from higher dimensions, they established an explicit scaling form for the free energy density, which simultaneously consists of a scaling term for the Gaussian fixed point and another term with multiplicative logarithmic corrections. In particular, they conjectured that the finite-size critical two-point correlation exhibits a two-length behavior, which is governed by Gaussian fixed point at shorter distance, and enters a plateau at larger distance whose height decreases with system size in a power law corrected by a logarithmic exponent.
On this basis, the FSS of various macroscopic quantities were predicted. They then carried out extensive Monte Carlo simulations for the n-vector model with n=1,2,3, and obtained solid evidence supporting the conjectured scaling forms from the FSS of the susceptibility, the magnetic fluctuations at non-zero Fourier modes, the Binder cumulant, as well as the two-point correlation at the distance of half of the linear system size. This is a significant step toward a complete solution of the logarithmic FSS at d=dc for systems having an upper critical dimensionality.
The study is not only of theoretical importance in model systems but also of practical relevance to a large number of experimental systems. It is noted that due to technological developments, the experimental realization of the O(n) model is now available in various physical systems including quantum magnetic materials, Josephson junction arrays, and ultracold atomic systems. According to the quantum-to-classical mapping, the three-dimensional quantum O(n) systems are at the upper critical dimensionality.
More information: Jian-Ping Lv et al, Finite-size Scaling of O(n) Systems at the Upper Critical Dimensionality*, National Science Review (2020). DOI: 10.1093/nsr/nwaa212
Provided by Science China Press