The cascade to criticality
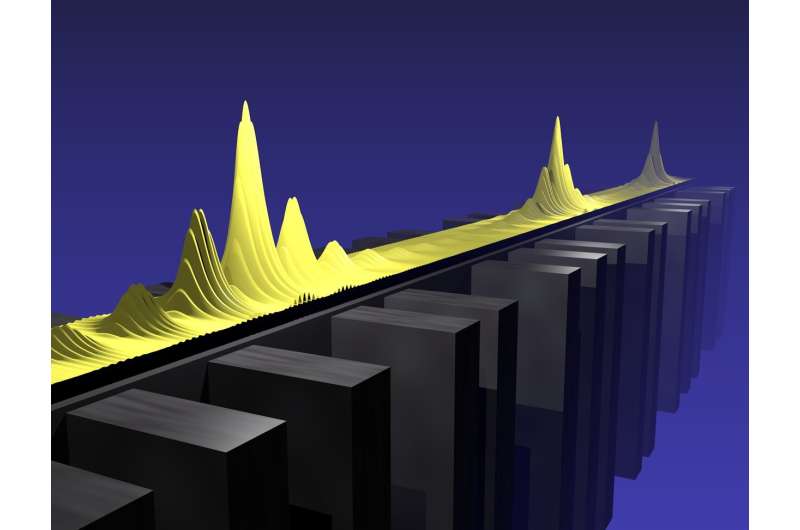
Combined theoretical and experimental work has resulted in a novel mechanism through which criticality emerges in quasiperiodic structures—a finding that provides unique insight into the physics on the middle ground between order and disorder.
Quasiperiodic structures, which are ordered but are not strictly periodic, are a source of extraordinary beauty in nature, art and science. For physicists, quasiperiodic order is both aesthetically and intellectually appealing. Numerous physical processes that are well described in periodic structures fundamentally change their character when they happen in quasiperiodic systems. Add quantum mechanics, and striking new phenomena can emerge that remain not fully understood. Writing in Nature Physics, an international team led by Oded Zilberberg of the Institute of Theoretical Physics at ETH Zurich and by CNRS physics researchers Jacqueline Bloch of the Université Paris-Saclay and Alberto Amo of Lille University, now describes combined theoretical and experimental work in which they establish versatile tools for exploring the behavior of quantum systems in a diverse range of one-dimensional quasiperiodic settings—and demonstrate the strength of their approach to uncover new physical mechanisms.
Intricate beauty
The essence, and beauty, of quasiperiodic structures can be grasped by considering floor plates. A floor can be readily tiled without gaps using identical pieces of, for example, triangular, square or hexagonal shape, repeating a simple pattern. But a plane surface can also be fully covered in non-repeating patterns, and that by using just two types of rhomboid tiles, as the English physicist and mathematician Roger Penrose has famously shown (see the figure). In that case, even if local configurations appear in different places, the overall pattern cannot be superimposed with itself by translation and rotation. As such, these systems occupy some sort of middle ground between periodic and randomly disordered structures.
On that middle ground, there is intriguing physics to be explored. Take a perfectly ordered crystal. There, the periodicity permits wavelike propagation of electrons through the material, for instance in a metal. If the crystalline perfection is perturbed by introducing disorder, the behavior changes. For low levels of disorder, the material still conducts, but less well. At some level of disorder though, the electrons stop propagating and become collectively localized, in a process known as Anderson localisation. For periodic lattices, this effect has first been described in 1958 (by 1977 Physics Nobel laureate Philip Anderson, who passed away on 29 March this year). But how such processes play out in quasiperiodic structures continues to be an area of active research.
Insightful interpolation
A wide range of unconventional physical phenomena has been described for quasiperiodic systems, but there exists no overarching framework for dealing with wave propagation in quasiperiodic structures. There are, however, various models that make it possible to study specific aspects of transport and localization. Two paradigmatic examples of such models are the Aubry-André and the Fibonacci models, each of which describes different physical phenomena, not least when it comes to localization properties.
In the Aubry-André model, there are two distinct parameter regions in which the particles can be in either 'extended' or localized states (in the same sense as electrons can either propagate through a material or be stuck in an insulating state). By contrast, in the Fibonacci model there is not one specific critical point separating the two regimes, but for any parameter the system is in such a critical state between localized and extended. Despite their sharply contrasting behaviors, the two models are connected to one another, and one can be continuously transformed into one another. This is something Zilberberg, then working at the Weizmann Institute of Science in Israel, had shown in breakthrough work with his colleague Yaacov Kraus in 2012. The question that remained was how the two so different localization behaviors are connected.

Piling up new insight
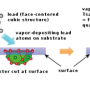
To answer that question, Zilberberg with his Ph.D. student Antonio Štrkalj and his former postdoc Jose Lado (now at Aalto University) teamed up with CNRS experimentalists Jacqueline Bloch and Alberto Amo and their Ph.D. student Valentin Goblot (now at the company STMicroelectronics). The French physicists had perfected a photonic platform—so-called cavity-polariton lattices—in which light can be guided through semiconductor nanostructures while experiencing interactions similar to those acting on electrons moving through a crystal. Importantly, they found ways to generate quasiperiodic modulations in their photonic wires that enabled them to implement experimentally, for the first time in any system, the Kraus-Zilberberg model. Optical spectroscopy experiments performed locally on these photonic quasi-crystals offer the exquisite possibility of directly imaging light localization in the systems.
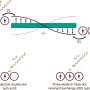
By combining their theoretical and experimental tools, the researchers were able to trace how the Aubry-André model evolves to become fully critical in the limit of the Fibonacci model. Counter naïve expectation, the team showed that this does not happen in a smooth way, but through a cascade of localization-delocalization transitions. Starting, for example, from the region of the Aubry-André model where particles are localized, at each step of the cascade process energy bands merge in a phase transition, during which particles are passing through the material. At the other side of the cascaded transition, the localization roughly doubles, sending the states of Aubry-André model gradually towards full criticality as it morphs into the Fibonacci model.
The situation bears some resemblance to what happens to a pile of rice as grains are added one by one. For some time, newly added grains will just sit where they landed. But once the slope at the landing site exceeds a critical steepness, a local avalanche is induced, leading to a rearrangement of parts of the pile surface. Repeating the process eventually leads to a stationary pile where one additional grain can trigger an avalanche on any of the relevant size scales—a 'critical' state. In the quasiperiodic systems, the situation is more complex because of the quantum nature of the particles involved, which means that these do not move like particles, but interfere like waves do. But in this setting as well, the evolution towards an overall critical state happens, as in the rice pile, through a cascade of discrete transitions.
With the theoretical description and experimental observation of this cascade to criticality, the teams have successfully connected quantum phenomena on two paradigmatic models of quasiperiodic chains, adding unique insight into the emergence of criticality. Moreover, they developed a flexible experimental platform for further explorations. The significance of these experiments goes firmly beyond light properties. The behavior of electrons, atoms and other quantum entities is governed by the same physics, which could inspire new ways of quantum control in devices. Just as the appeal of quasiperiodic patterns transcends disciplines, the potential to inspire scientific and eventually technological advances seems similarly boundless.
More information: V. Goblot et al, Emergence of criticality through a cascade of delocalization transitions in quasiperiodic chains, Nature Physics (2020). DOI: 10.1038/s41567-020-0908-7
Journal information: Nature Physics
Provided by ETH Zurich