How maths can answer questions we haven't thought of yet
Maths is considered an instrument that produces correct answers to our questions about the universe. For example, maths can predict correctly that if you have two apples and eat an apple a day, they will last you precisely two days.
However, sometimes maths produces answers that seem counterintuitive to our own experiences of the universe, like the Banach–Tarski paradox, which states that a solid ball can be cut into several pieces and these pieces can be assembled into two solid balls, each having the same size as the original ball.
Do these contradictions suggest that there's a crisis in maths, that it can't explain the mysteries of the universe? No. They just force us to reconsider how we approach these problems.
Making sense of the universe
Suppose you're on a seashore with a child, and you have a pair of binoculars. You hand the binoculars to the child and suggest that she look at seagulls. However, she is much more interested in you than seagulls, so within a minute she trains the binoculars on you, expecting to see a larger version of you, and she sees only a blur.
Is something wrong with either of you? No. Is something wrong with the binoculars. No. Your child simply uses the binoculars outside the range within which they can produce meaningful results. In the same way, counterintuitive statements in mathematics show us the limits of the useful range of using certain mathematical tools.
We all know one mathematical paradox from our childhood: you can't divide by zero. This is because numbers and arithmetic operations are all useful tools, and it is reasonable to combine these tools and use them together as far as possible.
However, mathematics is not one harmonious entity – its tools fit together reasonably well, but not perfectly well. We have to mind the gap between them. Division is a useful tool, and zero is a useful tool, but dividing by zero is beyond the useful range of division.
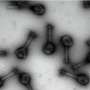
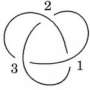
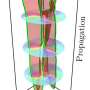
Aside from facts and paradoxes, mathematics can also produce unusual models which seem intentionally detached from the world that surrounds us. Let us consider one very simple example. The picture below shows a knotted string. Its ends are glued together to prevent it unknotting when pulled one way or another.
We cannot untie a knot like this just by gently pulling it, we have to cut it. However, an alternative approach asks whether a knot can be unknotted by considering it in some imaginary space instead of the usual space. For example, the knot in the picture above is a so-called slice knot, which can be unknotted easily if we observe it in four spatial dimensions, rather than the three-dimensional space we're used to.
Answering tomorrow's questions
Why is it important for mathematicians to produce these unusual models? One reason is to create an arsenal of mathematical models which can be used if science needs it in the future. In other words, some of these models can stop being fantastic and can start making perfect sense once our knowledge of the universe catches up.
Most famously, non-Euclidean geometry, which was developed as a thought experiment by mathematicians in the middle of the 19th century, argued that some straight lines may be curved. It became indispensable to the 20th-century discovery of the relativity theory, which argued that light, instead of travelling in a straight line, sometimes travels along a curve, or even around a circle.
There is also another reason to be aware of unusual mathematical models. Not all these models get a chance to become directly applied in experimental sciences, but they can all expand our imagination and suitably prepare us for accepting newly discovered scientific phenomena. This is important for appreciating modern science.
Some people don't understand or don't believe in the Big Bang. This is most probably because their imagination fails them when they try to imagine a universe without matter as we know it and without space as we know it. To imagine space that is not the same as we perceive it may be difficult. For instance, it is difficult to imagine that, contrary to our first-hand experience, the Earth is not flat.
Even if you know that Earth is a sphere, it may seem strange that there are places where people walk "upside down". If you realise that mathematicians constantly consider and successfully deal with models of space which defy our intuition, this can give you confidence that if need arises, both humankind and you personally can tackle questions which defy our comprehension of space.
Provided by The Conversation
This article was originally published on The Conversation. Read the original article.![]()