This math puzzle will help you plan your next party

Let's say you're planning your next party and agonizing over the guest list. To whom should you send invitations? What combination of friends and strangers is the right mix?
It turns out mathematicians have been working on a version of this problem for nearly a century. Depending on what you want, the answer can be complicated.
Our book, "The Fascinating World of Graph Theory," explores puzzles like these and shows how they can be solved through graphs. A question like this one might seem small, but it's a beautiful demonstration of how graphs can be used to solve mathematical problems in such diverse fields as the sciences, communication and society.
A puzzle is born
While it's well-known that Harvard is one of the top academic universities in the country, you might be surprised to learn that there was a time when Harvard had one of the nation's best football teams. But in 1931, led by All–American quarterback Barry Wood, such was the case.
That season Harvard played Army. At halftime, unexpectedly, Army led Harvard 13–0. Clearly upset, Harvard's president told Army's commandant of cadets that while Army may be better than Harvard in football, Harvard was superior in a more scholarly competition.
Though Harvard came back to defeat Army 14-13, the commandant accepted the challenge to compete against Harvard in something more scholarly. It was agreed that the two would compete – in mathematics. This led to Army and Harvard selecting mathematics teams; the showdown occurred in West Point in 1933. To Harvard's surprise, Army won.
The Harvard–Army competition eventually led to an annual mathematics competition for undergraduates in 1938, called the Putnam exam, named for William Lowell Putnam, a relative of Harvard's president. This exam was designed to stimulate a healthy rivalry in mathematics in the United States and Canada. Over the years and continuing to this day, this exam has contained many interesting and often challenging problems – including the one we describe above.
Red and blue lines
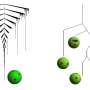
The 1953 exam contained the following problem (reworded a bit): There are six points in the plane. Every point is connected to every other point by a line that's either blue or red. Show that there are three of these points between which only lines of the same color are drawn.
In math, if there is a collection of points with lines drawn between some pairs of points, that structure is called a graph. The study of these graphs is called graph theory. In graph theory, however, the points are called vertices and the lines are called edges.
Graphs can be used to represent a wide variety of situations. For example, in this Putnam problem, a point can represent a person, a red line can mean the people are friends and a blue line means that they are strangers.
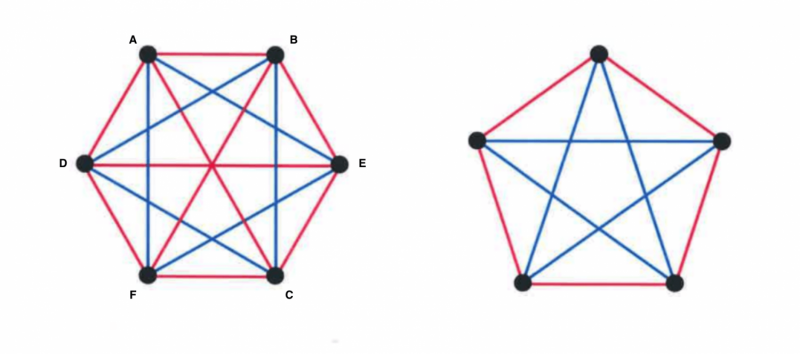
For example, let's call the points A, B, C, D, E, F and select one of them, say A. Of the five lines drawn from A to the other five points, there must be three lines of the same color.
Say the lines from A to B, C, D are all red. If a line between any two of B, C, D is red, then there are three points with only red lines between them. If no line between any two of B, C, D is red, then they are all blue.
What if there were only five points? There may not be three points where all lines between them are colored the same. For example, the lines A–B, B–C, C–D, D–E, E–A may be red, with the others blue.
From what we saw, then, the smallest number of people who can be invited to a party (where every two people are either friends or strangers) such that there are three mutual friends or three mutual strangers is six.
What if we would like four people to be mutual friends or mutual strangers? What is the smallest number of people we must invite to a party to be certain of this? This question has been answered. It's 18.
What if we would like five people to be mutual friends or mutual strangers? In this situation, the smallest number of people to invite to a party to be guaranteed of this is – unknown. Nobody knows. While this problem is easy to describe and perhaps sounds rather simple, it is notoriously difficult.
Ramsey numbers
What we have been discussing is a type of number in graph theory called a Ramsey number. These numbers are named for the British philosopher, economist and mathematician Frank Plumpton Ramsey.
Ramsey died at the age of 26 but obtained at his very early age a very curious theorem in mathematics, which gave rise to our question here. Say we have another plane full of points connected by red and blue lines. We pick two positive integers, named r and s. We want to have exactly r points where all lines between them are red or s points where all lines between them are blue. What's the smallest number of points we can do this with? That's called a Ramsey number.
For example, say we want our plane to have at least three points connected by all red lines and three points connected by all blue lines. The Ramsey number – the smallest number of points we need to make this happen – is six.
When mathematicians look at a problem, they often ask themselves: Does this suggest another question? This is what has happened with Ramsey numbers – and party problems.
For example, here's one: Five girls are planning a party. They have decided to invite some boys to the party, whether they know the boys or not. How many boys do they need to invite to be certain that there will always be three boys among them such that three of the five girls are either friends with all three boys or are not acquainted with all three boys? It's probably not easy to make a good guess at the answer. It's 41!
Very few Ramsey numbers are known. However, this doesn't stop mathematicians from trying to solve such problems. Often, failing to solve one problem can lead to an even more interesting problem. Such is the life of a mathematician.
Provided by The Conversation
This article was originally published on The Conversation. Read the original article.![]()