How do we know the universe is flat? Discovering the topology of the universe
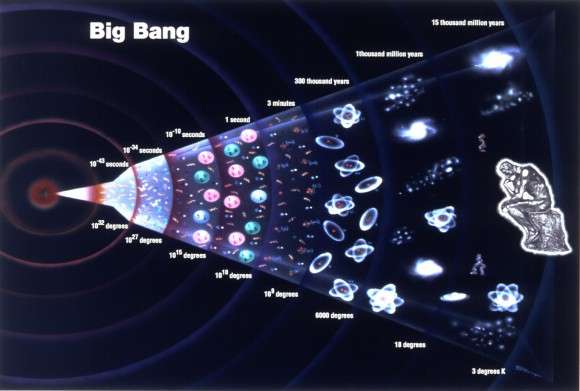
Whenever we talk about the expanding universe, everyone wants to know how this is going to end. Sure, they say, the fact that most of the galaxies we can see are speeding away from us in all directions is really interesting. Sure, they say, the Big Bang makes sense, in that everything was closer together billions of years ago.
But how does it end? Does this go on forever? Do galaxies eventually slow down, come to a stop, and then hurtle back together in a Big Crunch? Will we get a non-stop cycle of Big Bangs, forever and ever?
We've done a bunch of articles on many different aspects of this question, and the current conclusion astronomers have reached is that because the universe is flat, it's never going to collapse in on itself and start another Big Bang.
But wait, what does it mean to say that the universe is "flat"? Why is that important, and how do we even know?
Before we can get started talking about the flatness of the universe, we need to talk about flatness in general. What does it mean to say that something is flat?
If you're in a square room and walk around the corners, you'll return to your starting point having made four 90-degree turns. You can say that your room is flat. This is Euclidian geometry.
ut if you make the same journey on the surface of the Earth. Start at the equator, make a 90-degree turn, walk up to the North Pole, make another 90-degree turn, return to the equator, another 90-degree turn and return to your starting point.
In one situation, you made four turns to return to your starting point, in another situation it only took 3. That's because the topology of the surface you were walking on decided what happens when you take a 90-degree turn.
You can imagine an even more extreme example, where you're walking around inside a crater, and it takes more than four turns to return to your starting point.
Another analogy, of course, is the idea of parallel lines. If you fire off two parallel lines at the North pole, they move away from each other, following the topology of the Earth and then come back together.
Got that? Great.
Now, what about the universe itself? You can imagine that same analogy. Imaging flying out into space on a rocket for billions of light-years, performing 90-degree maneuvers and returning to your starting point.
You can't do it in three, or five, you need four, which means that the topology of the universe is flat. Which is totally intuitive, right? I mean, that would be your assumption.
But astronomers were skeptical and needed to know for certain, and so, they set out to test this assumption.
In order to prove the flatness of the universe, you would need to travel a long way. And astronomers use the largest possible observation they can make. The cosmic microwave background radiation, the afterglow of the Big Bang, visible in all directions as a red-shifted, fading moment when the universe became transparent about 380,000 years after the Big Bang.
When this radiation was released, the entire universe was approximately 2,700 C. This was the moment when it was cool enough for photons were finally free to roam across the universe. The expansion of the universe stretched these photons out over their 13.8 billion year journey, shifting them down into the microwave spectrum, just 2.7 degrees above absolute zero.
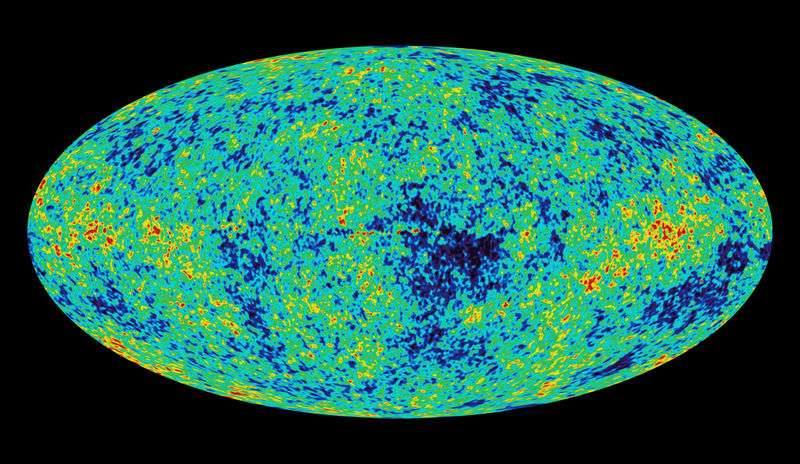
With the most sensitive space-based telescopes they have available, astronomers are able to detect tiny variations in the temperature of this background radiation.
And here's the part that blows my mind every time I think about it. These tiny temperature variations correspond to the largest scale structures of the observable universe. A region that was a fraction of a degree warmer become a vast galaxy cluster, hundreds of millions of light-years across.
The cosmic microwave background radiation just gives and gives, and when it comes to figuring out the topology of the universe, it has the answer we need. If the universe was curved in any way, these temperature variations would appear distorted compared to the actual size that we see these structures today.
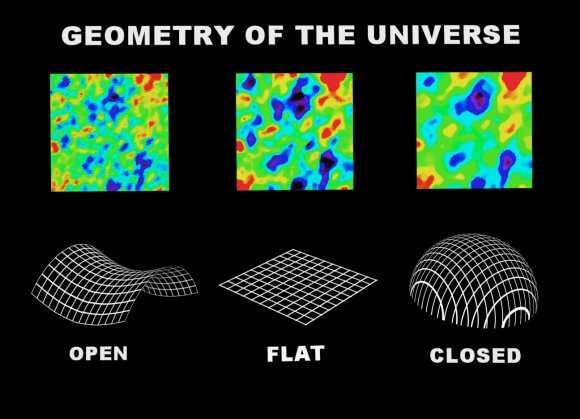
But they're not. To best of its ability, ESA's Planck space telescope, can't detect any distortion at all. The universe is flat.
Well, that's not exactly true. According to the best measurements astronomers have ever been able to make, the curvature of the universe falls within a range of error bars that indicates it's flat. Future observations by some super Planck telescope could show a slight curvature, but for now, the best measurements out there say… flat.
We say that the universe is flat, and this means that parallel lines will always remain parallel. 90-degree turns behave as true 90-degree turns, and everything makes sense.
But what are the implications for the entire universe? What does this tell us?
Unfortunately, the biggest thing is what it doesn't tell us. We still don't know if the universe is finite or infinite. If we could measure its curvature, we could know that we're in a finite universe, and get a sense of what its actual true size is, out beyond the observable universe we can measure.
We know that the volume of the universe is at least 100 times more than we can observe. At least. If the flatness error bars get brought down, the minimum size of the universe goes up.
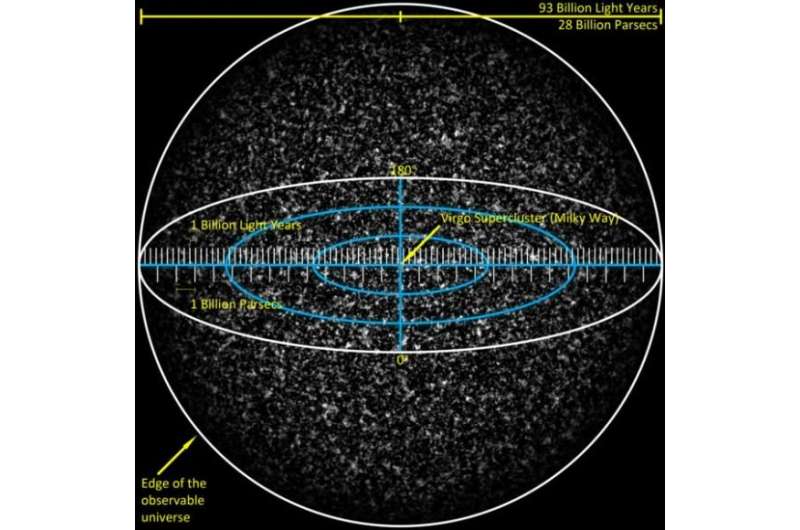
And remember, an infinite universe is still on the table.
Another thing this does, is that it actually causes a problem for the original Big Bang theory, requiring the development of a theory like inflation.
Since the universe is flat now, it must have been flat in the past, when the universe was an incredibly dense singularity. And for it to maintain this level of flatness over 13.8 billion years of expansion, in kind of amazing.
In fact, astronomers estimate that the universe must have been flat to 1 part within 1×1057 parts.
Which seems like an insane coincidence. The development of inflation, however, solves this, by expanding the universe an incomprehensible amount moments after the Big Bang. Pre and post inflation universes can have vastly different levels of curvature.
In the olden days, cosmologists used to say that the flatness of the universe had implications for its future. If the universe was curved where you could complete a full journey with less than four turns, that meant it was closed and destined to collapse in on itself.
And it was more than four turns, it was open and destined to expand forever.
Well, that doesn't really matter any more. In 1998, the astronomers discovered dark energy, which is this mysterious force accelerating the expansion of the universe. Whether the universe is open, closed or flat, it's going to keep on expanding. In fact, that expansion is going to accelerate, forever.
I hope this gives you a little more understanding of what cosmologists mean when they say that the universe is flat. And how do we know it's flat? Very precise measurements in the cosmic microwave background radiation.
Source: Universe Today



















