February 7, 2017 feature
Never-before-seen topological solitons experimentally realized in liquid crystals
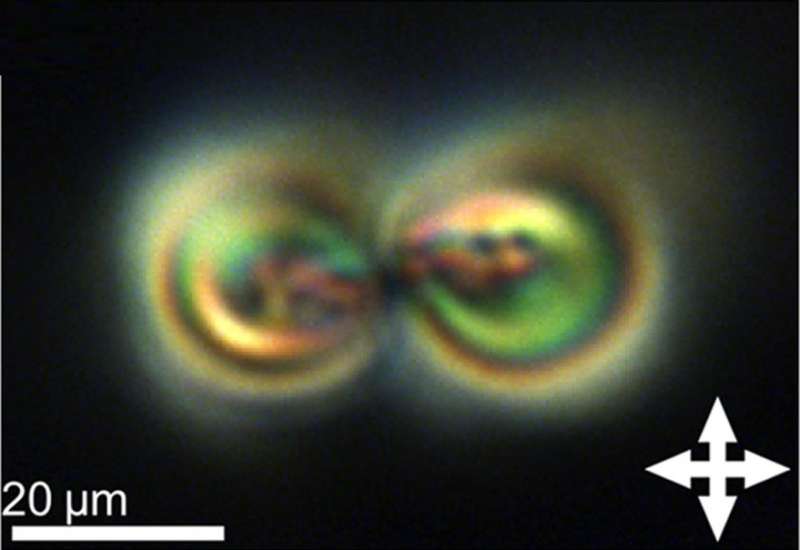
(Phys.org)—Physicists have discovered that dozens of 3-D knotted structures called "topological solitons," which have remained experimentally elusive for hundreds of years, can be created and frozen for long periods of time in liquid crystals like those used in electronic displays. Until now, topological solitons have been realized only in a few experiments, and for such a short time that it has been impossible to study them in any detail.
The new results may change all that, as they provide a way to produce a wide diversity of long-lasting topological solitons that can be studied with microscopes and, perhaps one day, play a role in novel optical and electrical applications.
The researchers, Paul J. Ackerman and Ivan I. Smalyukh at the University of Colorado, Boulder, have published a paper on the experimental realization of topological solitons in a recent issue of Physical Review X.
"Our work establishes experimental and numerical approaches for detailed studies of 3-D topological solitons, with the great advantage of enabling a direct comparison between experimental and theoretical results and with a potential impact on many branches of physics and the mathematical field of topology," Smalyukh told Phys.org. "Our work not only experimentally demonstrates 3-D topological solitons that mathematicians and theoretical physicists envisaged previously, but also reveals a series of solitonic structures that have not been anticipated."
Knotted background
Interest in topological solitons dates back to the early 1800s, when the mathematician Carl Friedrich Gauss suggested that the lines of magnetic and electric fields form 3-D knots that might behave like particles. Later, Lord Kelvin and others considered knotted vortices as an early model of the atom, in which the knots' properties could explain the chemical properties of the different elements.
Currently, many models in physics and cosmology involve topological solitons—for instance, models of condensed matter systems, elementary particles, magnetic monopoles, and magnetic particles called skyrmions that play a role in the emerging field of spintronics.
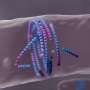
What exactly are topological solitons? If you take two or more circular rings, link them together to make a chain, then distort the rings by twisting and pulling on them as if they were made of putty, and finally embed the entire structure into a background surface, the result would look like a topological soliton. Describing these objects in more precise detail requires defining them as four-dimensional objects called "three-spheres," and then converting these four-dimensional objects into three-dimensional objects using a mathematical technique called Hopf mapping. It's these 3-D objects, called "preimages," that are the linked rings shown in visual representations.
One of the reasons why topological solitons are so difficult to experimentally realize is that they correspond to a physical system's lowest energy state in order to be stable. For this reason, they have been demonstrated only as transient structures in liquid crystals. It's also possible that topological solitons may exist in another medium, chiral ferromagnets, but a lack of experimental imaging techniques prevents researchers from observing them.

Freezing knots
In the new study, the researchers developed a method to "freeze" topological solitons in a solid film of chiral nematic liquid crystals through a polymerization process involving low levels of ultraviolet light, along with heating and cooling. To enable the experiment to be broadly accessible, the researchers used commercially available liquid crystals, to which they added chiral dopants. Using optical tweezers to generate and manipulate patterns in the pre-frozen liquid crystals, the researchers could also control the types of topological solitons being made.
After the topological solitons are frozen into the liquid crystals, the researchers can study them using an optical microscope—specifically, a three-photon excitation fluorescence polarizing microscope, which produces an optical signal that can be used to construct 3-D images of the solitons.
In the second part of their study, the researchers showed how this data could then be used to make numerical simulations corresponding to the highly complex physical structures. This process is based on analyzing the energetically favorable twisting patterns that minimize the liquid crystals' elastic free energy. Essentially, this process of converting the experimental structures (preimages) to numerical models is analogous to the mathematical Hopf mapping of 3-D objects (preimages) to four dimensions.
Potential applications
The ability to generate long-lasting topological solitons also opens the doors to potential applications. One idea is to take advantage of the fact that different topological solitons have distinct optical properties, which could be used in optical devices that shift the phase of light, as well as in pixels for optical displays. In addition, if the topological solitons identified here in liquid crystals also exist in solid ferromagnets, the researchers expect that they could potentially revolutionize the field of skyrmionics, in which skyrmions could be used to construct magnetic devices, such as data storage and logic.
"The large variety of localized long-term stable topological solitons, combined with the unique electro-optic properties of the liquid crystal host medium, will inevitably lead to technological applications, such as electro-optic devices and bistable information displays," Ackerman said. "A broad spectrum of new opportunities also emerge on the fundamental side, where our research group will work to establish how different topological solitons can transform one to another and also how the solitons with large Hopf index values can be experimentally realized."
Overall, one of the biggest advantages of the new method is that it provides a much more comprehensive, detailed analysis of topological soliton preimages than other construction methods. As a result, the new method uncovers small details in the topology that could easily be missed otherwise, such as subtle differences between very similar structures that could have been mistaken to be the same structure. The results show that topological solitons are more complex and diverse than previous evidence could show, and indicate that many more of these structures are still waiting to be discovered.
"An infinitely large number of topological solitons may potentially exist, especially when considering different physical systems," Smalyukh said.
More information: Paul J. Ackerman and Ivan I. Smalyukh. "Diversity of Knot Solitons in Liquid Crystals Manifested by Linking of Preimages in Torons and Hopfions." Physical Review X. DOI: 10.1103/PhysRevX.7.011006
Journal information: Physical Review X
© 2017 Phys.org