When is a coffee mug a donut? Topology explains it

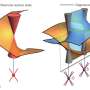
A topologist is a person who cannot tell the difference between a coffee mug and a donut—so goes a joke about a little-known scientific field crowned Tuesday with a Nobel Physics Prize.
The quip describes it perfectly: topology explains how a material's shape can be completely deformed into new one without losing its core properties.
In the metaphor, the mug and the donut are one and the same. If they were made out of rubber, one could be twisted and stretched into the shape of the other without changing its essence.
The two are considered topologically equivalent as each has a hole—the ear of the mug and the centre of the donut.
"You can put your finger through the hole in a teacup handle, but you can't put it through a potato, so these are two different categories of topological objects," explained Manuel Asorey of the University of Zaragoza's department of theoretical physics.
A strange universe of fundamental shapes long existing only in mathematics, the field was introduced into the physics realm just a few decades ago.
Indeed, in the mid-20th century theoretical physicist George Gamow said topology was one of two mathematical concepts, along with number theory, that would never apply to physics.

Gamow was wrong.
Today, topology has burgeoned into a wide range of physics sub-fields promising a host of practical applications ranging from supercomputing to superconductors.
By shaping materials into "topological states," scientists hope one day to transport energy or information farther and faster than possible today.
"Pioneers glimpsed that topology could have some relevance to physics," said Asorey.
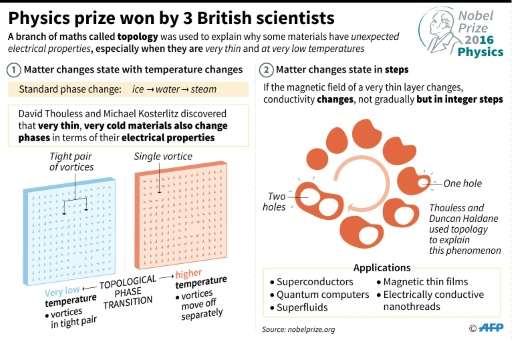
"But the real practical applications became apparent because of these three gentlemen,"—Nobel laureates David Thouless, Duncan Haldane and Michael Kosterlitz—who "realised that topology was not something visible," he told AFP.
"Now people are generalising these ideas to many other fields of physics."
Robustness is key
Sometimes referred to as "rubber sheet geometry", topology in physics remains in the theoretical and experimental realm for now.
But its principles are widely expected to find practical and commercial application within a decade or two, particularly in the quantum sphere of electronics and computing.
It is hoped, for example, that new materials emerging from this research will use much less electricity.
The key virtue of topological materials is that they "remain robust regardless of the deforming forces being applied to them," said David Carpentier, a physicist at France's CNRS research institute.
"It is exactly this robustness in topology that is being examined as a basis for constructing the quantum computers of the future."

Quantum computers, still on the drawing board, promise superfast processing speeds using the properties of subatomic particles that exist in more than one state at once.
But they pose a high risk of overheating, which is where topological insulators with an inherent stability would come in very handy.
"Two years ago, I would have said it would take at least two decades to see something on the supermarket shelf" resulting from topology research, Asorey said.
"Today, I would say one decade, maybe less."
For Nathan Goldman of the Free University of Brussels, "we are still a ways from technological applications" or a revolution in computing.
"The next step will be to create these objects in the lab and try to manipulate them, performing very simple operations."
© 2016 AFP