Will computers replace humans in mathematics?

Computers can be valuable tools for helping mathematicians solve problems but they can also play their own part in the discovery and proof of mathematical theorems.
Perhaps the first major result by a computer came 40 years ago, with proof for the four-color theorem – the assertion that any map (with certain reasonable conditions) can be coloured with just four distinct colours.
This was first proved by computer in 1976, although flaws were later found, and a corrected proof was not completed until 1995.
In 2003, Thomas Hales, of the University of Pittsburgh, published a computer-based proof of Kepler's conjecture that the familiar method of stacking oranges in the supermarket is the most space-efficient way of arranging equal-diameter spheres.
Although Hales published a proof in 2003, many mathematicians were not satisfied because the proof was accompanied by two gigabytes of computer output (a large amount at the time), and some of the computations could not be certified.
In response, Hales produced a computer-verified formal proof in 2014.
The new kid on the block
The latest development along this line is the announcement this month in Nature of a computer proof for what is known as the Boolean Pythagorean triples problem.
The assertion here is that the integers from one to 7,824 can be coloured either red or blue with the property that no set of three integers a, b and c that satisfy a2 + b2 = c2 (Pythagoras's Theorem where a, b and c form the sides of a right triangle) are all the same colour. For the integers from one to 7,825, this cannot be done.
Even for small integers, it is hard to find a non-monochrome colouring. For instance, if five is red then one of 12 or 13 must be blue, since 52 + 122 = 132; and one of three or four must also be blue, since 32 + 42 = 52. Each choice has many constraints.
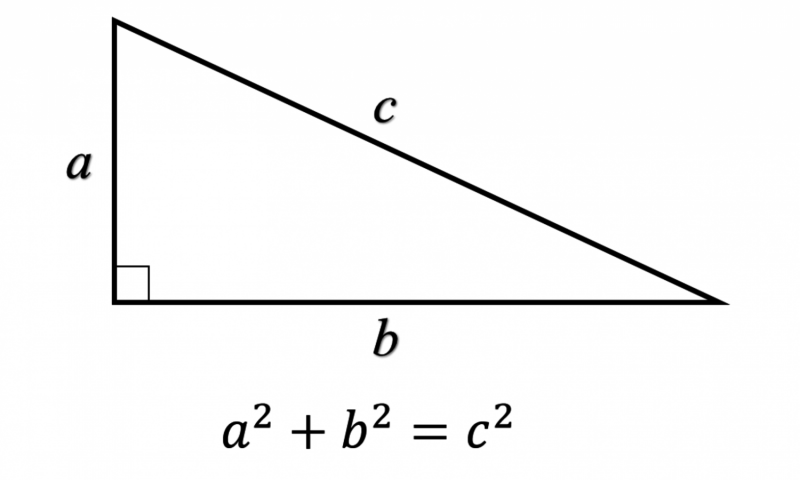
As it turns out, the number of possible ways to colour the integers from one to 7,825 is gigantic – more than 102,300 (a one followed by 2,300 zeroes). This number is far, far greater than the number of fundamental particles in the visible universe, which is a mere 1085.
But the researchers were able to sharply reduce this number by taking advantage of various symmetries and number theory properties, to "only" one trillion. The computer run to examine each of these one trillion cases required two days on 800 processors of the University of Texas' Stampede supercomputer.
While direct applications of this result are unlikely, the ability to solve such difficult colouring problems is bound to have implications for coding and for security.
The Texas computation, which we estimate performed roughly 1019 arithmetic operations, is still not the largest mathematical computation. A 2013 computation of digits of pi2 by us and two IBM researchers did twice this many operations.
The Great Internet Mersenne Prime Search (GIMPS), a global network of computers search for the largest known prime numbers, routinely performs a total of 450 trillion calculations per second, which every six hours exceeds the number of operations performed by the Texas calculation.
In computer output, though, the Texas calculation takes the cake for a mathematical computation – a staggering 200 terabytes, namely 2✕1014 bytes, or 30,000 bytes for every human being on Earth.
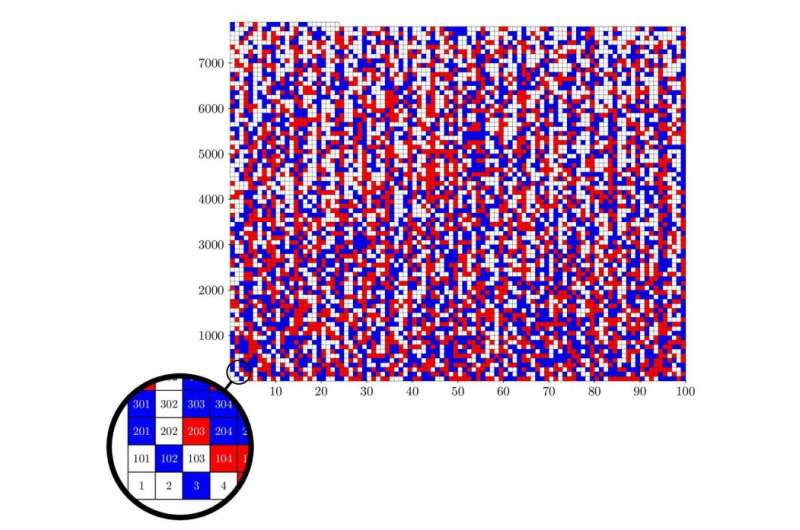
How can one check such a sizeable output? Fortunately, the Boolean Pythagorean triple program produced a solution (shown in the image, above) that can be checked by a much smaller program.
This is akin to factoring a very large number c into two smaller factors a and b by computer, so that c = a ✕ b. It is often quite difficult to find the two factors a and b, but once found, it is a trivial task to multiply them together and verify that they work.
Are mathematicians obsolete?
So what do these developments mean? Are research mathematicians soon to join the ranks of chess grandmasters, Jeopardy champions, retail clerks, taxi drivers, truck drivers, radiologists and other professions threatened with obsolescence due to rapidly advancing technology?
Not quite. Mathematicians, like many other professionals, have for the large part embraced computation as a new mode of mathematical research, a development known as experimental mathematics, which has far-reaching implications.

So what exactly is experimental mathematics? It is best defined as a mode of research that employs computers as a "laboratory," in the same sense that a physicist, chemist, biologist or engineer performs an experiment to, for example, gain insight and intuition, test and falsify conjecture, and confirm results proved by conventional means.
We have written on this topic at some length elsewhere – see our books and papers for full technical details.
In one sense, there there is nothing fundamentally new in the experimental methodology of mathematical research. In the third century BCE, the great Greek mathematician Archimedes wrote:
For it is easier to supply the proof when we have previously acquired, by the [experimental] method, some knowledge of the questions than it is to find it without any previous knowledge.
Galileo once reputedly wrote:
All truths are easy to understand once they are discovered; the point is to discover them.
Carl Friederich Gauss, 19th century mathematician and physicist, frequently employed computations to motivate his remarkable discoveries. He once wrote:
I have the result, but I do not yet know how to get [prove] it.
Computer-based experimental mathematics certainly has technology on its side. With every passing year, computer hardware advances with Moore's Law, and mathematical computing software packages such as Maple, Mathematica, Sage and others become ever more powerful.
Already these systems are powerful enough to solve virtually any equation, derivative, integral or other task in undergraduate mathematics.
So while ordinary human-based proofs are still essential, the computer leads the way in assisting mathematicians to identify new theorems and chart a route to formal proof.
What's more, one can argue that in many cases computations are more compelling than human-based proofs. Human proofs, after all, are subject to mistakes, oversights, and reliance on earlier results by others that may be unsound.
Andrew Wiles' initial proof of Fermat's Last Theorem was later found to be flawed. This was fixed later.
Along this line, recently Alexander Yee and Shigeru Kondo computed 12.1 trillion digits of pi. To do this, they first computed somewhat more than 10 trillion base-16 digits, then they checked their computation by computing a section of base-16 digits near the end by a completely different algorithm, and compared the results. They matched perfectly.
So which is more reliable, a human-proved theorem hundreds of pages long, which only a handful of other mathematicians have read and verified in detail, or the Yee-Kondo result? Let's face it, computation is arguably more reliable than proof in many cases.
What does the future hold?
There is every indication that research mathematicians will continue to work in respectful symbiosis with computers for the foreseeable future. Indeed, as this relationship and computer technology mature, mathematicians will become more comfortable leaving certain parts of a proof to computers.
This very question was discussed in a June 2014 panel discussion by the five inaugural Breakthrough Prize in Mathematics recipients for mathematics. The Australian-American mathematician Terence Tao expressed their consensus in these terms:
Computers will certainly increase in power, but I expect that much of mathematics will continue to be done with humans working with computers.
So don't toss your algebra textbook quite yet. You will need it!
Source: The Conversation
This article was originally published on The Conversation. Read the original article.
![]()