How the hidden mathematics of living cells could help us decipher the brain
Given how much they can actually do, computers have a surprisingly simple basis. Indeed, the logic they use has worked so well that we have even started to think of them as analogous to the human brain. Current computers basically use two basic values – 0 (false) and 1 (true) – and apply simple operations like "and", "or" and "not" to compute with them. These operations can be combined and scaled up to represent virtually any computation.
This "binary "or "Boolean" logic was introduced by George Boole in 1854 to describe what he called "the laws of thought". But the brain is far from a binary logic device. And while programmes such as the Human Brain Project seek to model the brain using computers, the notion of what computers are is also constantly changing.
So will we ever be able to model something as complex as the human brain using computers? After all, biological systems use symmetry and interaction to do things that even the most powerful computers cannot do – like surviving, adapting and reproducing. This is one reason why binary logic often falls short of describing how living things or human intelligence work. But our new research suggests there are alternatives: by using the mathematics that describe biological networks in the computers of the future, we may be able to make them more complex and similar to living systems like the brain.
Living organisms do not live in a world of zeroes and ones. And if binary logic doesn't naturally describe their activity, what kind of mathematics does? I was involved in an international project which studied whether mathematical structures called "Simple Non-Abelian Groups" (SNAGs) may describe complex processes in living cells. SNAGs are commonly in mathematics and physics, and are based on the principles of symmetry and interaction. SNAGs offer a potentially powerful alternative to binary logic for computation.
Helpful SNAGs
There are infinitely many kinds of SNAGs. They were conjured by the brilliant 19th-century French mathematician Évariste Galois, who tragically died aged 20 in a fatal duel over a romantic interest. Indeed, he wrote much of his ground-breaking theory during a feverish night before the duel.
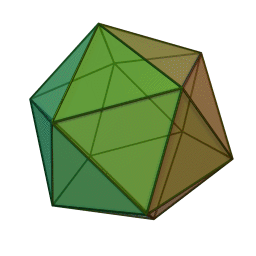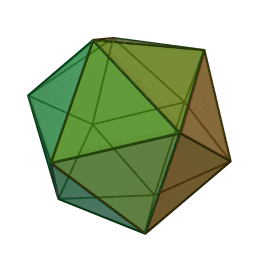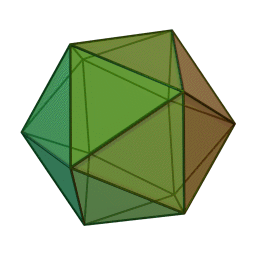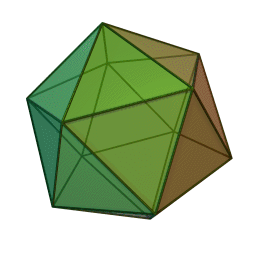
The smallest SNAG – A5 – describes the symmetries of two beautiful 3D shapes known since the time of the ancient Greeks: the icosahedron (made of 20 triangles) and the dodecahedron (made of 12 pentagons). SNAGs can be thought of as the "multiplication tables" of how symmetries interact, rather than for how to multiply numbers.
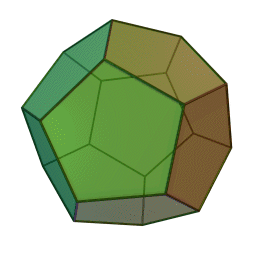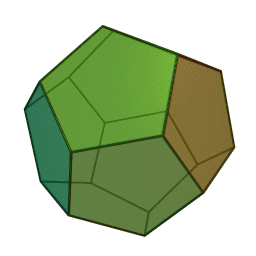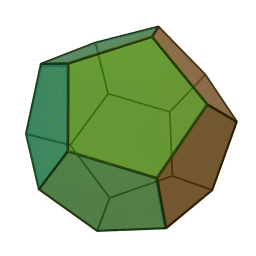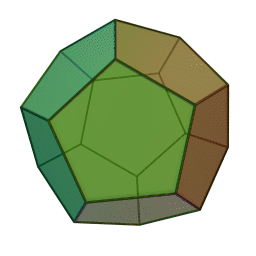
The structure of SNAGs is a natural kind of basis for computation that is just as powerful as binary logic, but presents a very different view about which computations are easy. To compute with SNAGs, nature (or humans or future computers) can use sequences of SNAG symmetries combined according to the rules. Patterns of events and interactions determine which symmetries occur in the sequence's variable positions.
Symmetries in nature
We have for the first time shown that there are SNAGs hidden in common biological networks. To do this, we analysed the internal workings of cells (their gene regulation and metabolism) using mathematics, computers and models from systems biology. We found that SNAG symmetries accurately describe potential activities in the genetic regulatory network that controls a cell's response to certain kinds of stress – such as radiation and DNA damage. This may be hugely important as it means SNAGs can describe cellular processes intimately involved in self-repair, "cell suicide", and cancer.
The specific SNAG involved in this gene network is A5. The 60 symmetries in this case are the result of particular sequences of manipulations by the cell's genetic regulatory network to transform ensembles of proteins into other forms. For example, when a set of five concentration levels of proteins is manipulated, it can be transformed to another set. When this is done many times, it can break some of the proteins down, join some together or synthesise new types of proteins. But after a specific number of manipulations the original five concentration levels of proteins will eventually return.
It doesn't stop at cellular damage control processes. We have also shown mathematically that nearly all biological reaction networks must have numerous embedded SNAG components. However, lab work is still needed to explain how and to what extent cells exploit SNAGs in their activity.
Computation with SNAGs has never yet been exploited in conventional computers, but we are hoping to use it. In the future, new kinds of computers and software systems may deploy resources the way some living organisms do, in robust adaptive responses. Driven by interaction with their environment, including human users, they could grow new structures, divide up tasks among different types of computational "cells" such as hardware units or software processes, allow old structures to wither and be reabsorbed if unused.
Understanding how living things and brains use interaction-based computations, which are all around us, may radically reshape not only our computers and the internet, but the existing models of the brain and living organisms. SNAG-based computations may finally help us build better and more predictive working models of cells and of the brain. But we have only sighted the first examples, and so have a long way to go. After all, as Shakespeare and this discovery of SNAG-computation in cells remind us: "There are more things in heaven and earth, Horatio, than are dreamt of in your philosophy."
Source: The Conversation
This article was originally published on The Conversation. Read the original article.
![]()