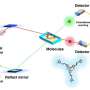
May 27, 2015 feature
Quantum computer emulated by a classical system

(Phys.org)—Quantum computers are inherently different from their classical counterparts because they involve quantum phenomena, such as superposition and entanglement, which do not exist in classical digital computers. But in a new paper, physicists have shown that a classical analog computer can be used to emulate a quantum computer, along with quantum superposition and entanglement, with the result that the fully classical system behaves like a true quantum computer.
Physicist Brian La Cour and electrical engineer Granville Ott at Applied Research Laboratories, The University of Texas at Austin (ARL:UT), have published a paper on the classical emulation of a quantum computer in a recent issue of The New Journal of Physics. Besides having fundamental interest, using classical systems to emulate quantum computers could have practical advantages, since such quantum emulation devices would be easier to build and more robust to decoherence compared with true quantum computers.
"We hope that this work removes some of the mystery and 'weirdness' associated with quantum computing by providing a concrete, classical analog," La Cour told Phys.org. "The insights gained should help develop exciting new technology in both classical analog computing and true quantum computing."
As La Cour and Ott explain, quantum computers have been simulated in the past using software on a classical computer, but these simulations are merely numerical representations of the quantum computer's operations. In contrast, emulating a quantum computer involves physically representing the qubit structure and displaying actual quantum behavior. One key quantum behavior that can be emulated, but not simulated, is parallelism. Parallelism allows for multiple operations on the data to be performed simultaneously—a trait that arises from quantum superposition and entanglement, and enables quantum computers to operate at very fast speeds.
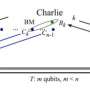
To emulate a quantum computer, the physicists' approach uses electronic signals to represent qubits, in which a qubit's state is encoded in the amplitudes and frequencies of the signals in a complex mathematical way. Although the scientists use electronic signals, they explain that any kind of signal, such as acoustic and electromagnetic waves, would also work.
Even though this classical system emulates quantum phenomena and behaves like a quantum computer, the scientists emphasize that it is still considered to be classical and not quantum.
"This is an important point," La Cour explained. "Superposition is a property of waves adding coherently, a phenomenon that is exhibited by many classical systems, including ours.
"Entanglement is a more subtle issue," he continued, describing entanglement as a "purely mathematical property of waves."
"Since our classical signals are described by the same mathematics as a true quantum system, they can exhibit these same properties."
He added that this kind of entanglement does not violate Bell's inequality, which is a widely used way to test for entanglement.
"Entanglement as a statistical phenomenon, as exhibited by such things as violations of Bell's inequality, is rather a different beast," La Cour explained. "We believe that, by adding an emulation of quantum noise to the signal, our device would be capable of exhibiting this type of entanglement as well, as described in another recent publication."
In the current paper, La Cour and Ott describe how their system can be constructed using basic analog electronic components, and that the biggest challenge is to fit a large number of these components on a single integrated circuit in order to represent as many qubits as possible. Considering that today's best semiconductor technology can fit more than a billion transistors on an integrated circuit, the scientists estimate that this transistor density corresponds to about 30 qubits. An increase in transistor density of a factor of 1000, which according to Moore's law may be achieved in the next 20 to 30 years, would correspond to 40 qubits.
This 40-qubit limit is also enforced by a second, more fundamental restriction, which arises from the bandwidth of the signal. The scientists estimate that a signal duration of a reasonable 10 seconds can accommodate 40 qubits; increasing the duration to 10 hours would only increase this to 50 qubits, and a one-year duration would only accommodate 60 qubits. Due to this scaling behavior, the physicists even calculated that a signal duration of the approximate age of the universe (13.77 billion years) could accommodate about 95 qubits, while that of the Planck time scale (10-43 seconds) would correspond to 176 qubits.
Considering that thousands of qubits are needed for some complex quantum computing tasks, such as certain encryption techniques, this scheme clearly faces some insurmountable limits. Nevertheless, the scientists note that 40 qubits is still sufficient for some low-qubit applications, such as quantum simulations. Because the quantum emulation device offers practical advantages over quantum computers and performance advantages over most classical computers, it could one day prove very useful. For now, the next step will be building the device.
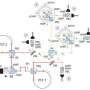
"Efforts are currently underway to build a two-qubit prototype device capable of demonstrating entanglement," La Cour said. "The enclosed photo [see above] shows the current quantum emulation device as a lovely assortment of breadboarded electronics put together by one of my students, Mr. Michael Starkey. We are hoping to get future funding to support the development of an actual chip. Leveraging quantum parallelism, we believe that a coprocessor with as few as 10 qubits could rival the performance of a modern Intel Core at certain computational tasks. Fault tolerance is another important issue that we studying. Due to the similarities in mathematical structure, we believe the same quantum error correction algorithms used to make quantum computers fault tolerant could be used for our quantum emulation device as well."
More information: Brian R. La Cour and Granville E. Ott. "Signal-based classical emulation of a universal quantum computer." New Journal of Physics. DOI: 10.1088/1367-2630/17/5/053017
Journal information: New Journal of Physics
© 2015 Phys.org