The legacy of John Nash and his equilibrium theory
The American mathematician John Nash, who died in a taxi accident at the weekend, is probably best known to the wider public through Russell Crowe's portrayal of him in the 2001 movie A Beautiful Mind.
His career in academia was glittering – he was awarded the Nobel Prize for Economics in 1994 and only this year he won the Abel Prize, often regarded as mathematics' own Nobel Prize.
Although his achievements spanned a huge number of fields in the mathematical sciences, he will likely be best remembered for his work in the development of game theory. His work in this area (to quote fellow Nobel Economics laureate Roger Myerson):
[…] had a fundamental and pervasive impact in economics and the social sciences which is comparable to that of the discovery of the DNA double helix in the biological sciences.
If anything, this quote slightly undersells the impact of what is arguably the most wide-ranging branch of 20th-century applied mathematics. Five of the last ten awards of the Nobel Prize in Economics have been to game theorists and it is now a bedrock in the life sciences, with major breakthroughs spanning evolutionary biology and studies in animal community behaviour.
What is game theory?
In its purest sense, game theory is the study of models of conflict or co-operation between intelligent decision-makers. Everything from the functioning of ant colonies to which products consumers might buy has been explained with this mathematical framework.
Nash's work in game theory began with his PhD, awarded by Princeton University in 1950. (Legend has it that his recommendation letter to Princeton's Graduate School was one simple sentence: "This man is a genius.")
The field predates Nash's own contributions, dating back at least to John von Neumann's work between the 1920s and 1940s and arguably to work in the 18th century which we would now classify as game theory.
Why then is the field so closely associated with Nash and why is he its most celebrated researcher?
The Nash equilibrium
Nash's most fundamental contribution to game theory was in opening the field up to a wider range of applications and different scenarios to be studied. Prior to his work, the field was very much concerned with a certain subset of problems, subject to very restrictive conditions.
By relaxing these and demonstrating the applicability of these concepts much more broadly, he took the discipline outside of its previously narrow focus. Without his breakthrough, much of what followed in game theory might not have been possible.
His most lasting legacy bears his name. He proved that in any game where a finite number of players each has a finite number of choices, there is at least one position from which no single player alone can improve his/her position by changing strategy.
Such a point is called a "Nash equilibrium". The proof is, in the words of the economist Samuel Bowles, that there is always "a situation in which everybody is doing the best they can, given what everybody else is doing".
But here's the rub: a Nash equilibrium does not necessarily mean that the best outcome for anyone is obtained. It simply means that no individual can improve his or her position, given they're unable to change the choices of other.
Prisoner's dilemma
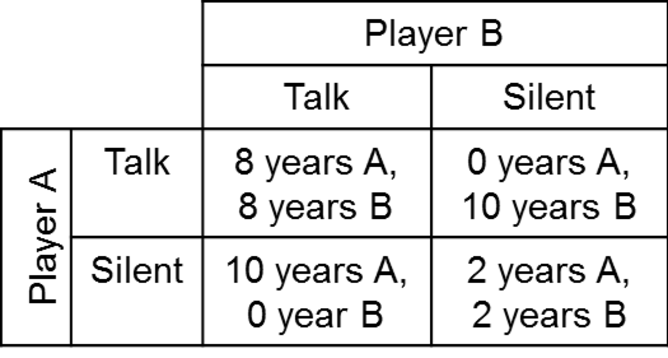
In the famous case of the Prisoner's Dilemma, two suspects are arrested for a crime and interviewed separately, unable to speak to each other.
The police have enough evidence to charge them with a lesser crime and jail each for two years. They are both suspected of a more serious crime, which carries a ten year sentence.
The police offer each a two year reduction in whichever sentence he/she will receive if the suspect gives evidence against the other suspect.
So what should each do?
If the Suspect A talks, then Suspect B (who doesn't know what the other has done) will get ten years if he chooses to remain silent and eight years if he talks.
If the Suspect A remains silent, then Suspect B will get two years if he remains silent and will walk free if he talks. In either case, Suspect A cannot improve his own outcome by remaining silent rather than talking.
The Nash equilibrium for this problem is therefore that both suspects give evidence against the other. But this is not the optimal solution – they get eight years jail each as opposed to a potential two each – but it is the only position from which each prisoner cannot improve his position by changing.
More complex games can have more than one Nash equilibrium position, meaning that individuals with identical choices might have different "best decisions" depending on where they find themselves at a given time.
Meerkat survival
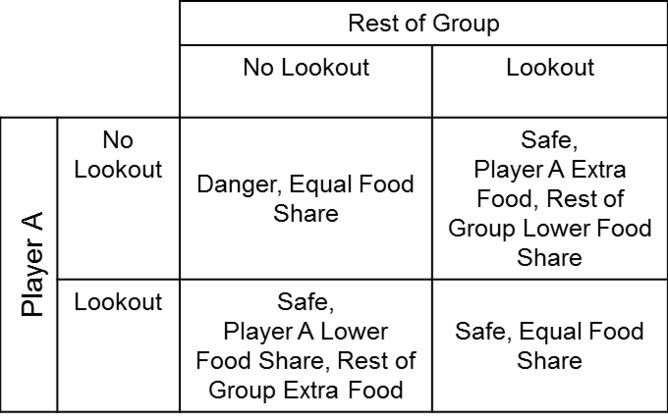
An example of this is used to explain the behaviour of meerkat communities. Consider a community under threat of being eaten by a large predator, but which is able to ensure the safety of every individual if at least one member stands on lookout.
There is an additional food supply which is shared between all members of the group together, but which is missed by any individuals on lookout. It is assumed that getting a share of the food is a small advantage over getting none, but potentially getting killed by the predator is a far worse negative than the food is a benefit.
What should each meerkat do?
If none is on lookout, the best move for each is to move to the lookout so that the worst-case scenario is avoided. If at least two are on lookout, the best move for each is to abandon this and return to the food, provided at least one remains.
This creates two Nash equilibria. The individuals in the group with extra food can only worsen their own situation by leaving to go on lookout. The last remaining individual on lookout can only worsen its own position by returning and leaving everyone at risk.
As an interesting side note, the movie A Beautiful Mind tried to illustrate a similar game to explain a Nash equilibrium, but it got its explanation woefully wrong and drew a conclusion from which any single player could improve his position by "defecting" from the co-operation. (So if just one single player changed his mind to the optimal position, then a Nash equilibrium would have been found.)
Nash's ongoing legacy
The legacy of Nash and his contribution to game theory will continue to fuel research in a vast array of different fields. As well as its ever-widening scope of applications, it remains a staple of many undergraduate and postgraduate curricula around the world.
I have taught workshops on simple examples and introduced the concept of a Nash equilibrium to first year mathematics undergraduates and it has been a lively and enjoyable topic, both for myself and for the students. Game theory can provide a fascinating mix of both seemingly obvious results plus some counter-intuitive ones, which always stir up spirited debate.
The impact of John Nash's initial work has been immense over the past 65 years. It seems certain that in his absence, the frameworks and mathematical language he refined and developed will continue to provide new insights into a diverse range of problems.
Whether the next major advance arising from his work comes in economics, in business, in ecology, or in evolutionary biology remains to be seen.
Stephen Woodcock is Lecturer in Mathematics at University of Technology, Sydney.
Source: The Conversation
This story is published courtesy of The Conversation (under Creative Commons-Attribution/No derivatives).
![]()