Working group explores the 'frustration' of spin glasses
Spin glasses are frustrating. Although the ideas have been around for decades and form the foundation of countless complex systems models, they have nonetheless resisted researchers' efforts to understand exactly how they work – something three SFI scientists hope to change starting with a five-day working group at SFI in July.
Spin models were originally introduced to study materials made up of tiny magnets with varying orientations – so-called spins – at the atomic scale. In a household fridge magnet, the "spins" prefer to be aligned, and that overall preference results in a magnetization useful for suspending a child's report card or grocery list.
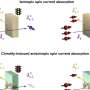
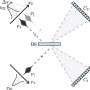
But the picture is not always so simple: In spin glasses each spin prefers to align with some of its neighbors, while being anti-aligned with others. These conflicting interactions can leave a spin in a quandary: which neighbors should it agree with?
This frustration – that is the technical term – and researchers' frustration when trying to understand spin glass dynamics is not limited to magnets, says SFI Omidyar Fellow Ruben Andrist, who along with SFI External Professors Jon Machta and Helmut Katzgraber is organizing the working group.
"It is not just a [problem in a] single field," Andrist says, citing examples in fields from quantum computing to voting models, where "frustrated spins" represent voters trying to decide between political parties. While there is inherent interest in solving such models, their complexity makes solving them very challenging, he says.
The working group will lead off with a basic question, he says: "Can we even make a statement about how computationally complex a problem typically is?" In the worst case, spin glass problems are among the hardest to solve, he says, but the typical case could be easier, and figuring that out would already be a step forward.
The group will review several recent developments in the field and, they hope, develop measures of difficulty that will aid researchers' efforts to study spin glasses across disciplinary boundaries.
Provided by Santa Fe Institute