Physicists propose measure of macroscopicity; Schrodinger's cat scores a 57

(Phys.org) —The size of an object can be measured in many ways, such as by its mass, volume, or even the number of atoms it contains. And when it comes to quantum physics, "macroscopic" objects are considered to be larger than "quantum" ones, since the former are usually described by classical laws and the latter by quantum laws. However, physicists have been challenging the boundary between these two realms by performing experiments that show that multiparticle objects can exist in quantum superpositions. But there has been no standard measure of macroscopicity until now, as a team of physicists has proposed that the macroscopicity of an object can be measured in terms of certain parameters of the experiment used to probe its quantum superposition, rather than as a single property of the object itself.

Physicists Stefan Nimmrichter of the University of Vienna, Austria, and Klaus Hornberger of the University of Duisburg-Essen, Germany, have published a paper on the new definition of macroscopicity in a recent issue of Physical Review Letters.

In the past, researchers have often measured an object's macroscopicity in terms of the number of atoms in the object. But different atoms are different sizes since they contain different numbers of subatomic particles, which raises the question of whether macroscopicity should be measured in terms of the total number of an object's protons, neutrons, and electrons, or even some other way entirely. As physicists continue to observe quantum effects such as superposition in larger objects, a standard measurement of macroscopicity is needed for comparing these results.

Rather than defining macroscopicity solely in terms of an object's composition, Nimmrichter and Hornberger's definition is based on the idea that quantum equations can be modified to make an object's state more classical. If an experiment can rule out some of these modifications, then it describes a larger quantum superposition and a more macroscopic object. The more modifications an experiment rules out, the more macroscopic the object is.

Several factors can help rule out modifications to achieve a large macroscopicity. For example, a superposition with a long coherence time and an object with a large mass both rule out modifications, among other factors. Taken together, all of these parameters yield a single number, μ, on a logarithmic scale that can be used to grade macroscopicity. On this scale, the superposition state of an object has the same macroscopicity as that of a single electron existing in a superposition for 10^μ seconds.

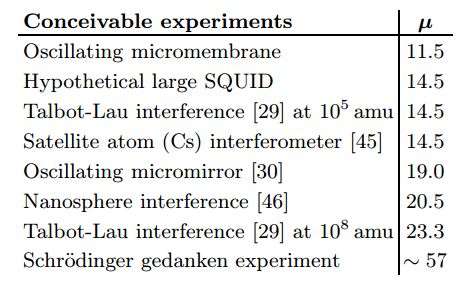
Based on this criteria, the physicists gave scores to some recent superposition experiments. The macroscopicity record score so far is 12, which was achieved by Nimmrichter, Hornberger, and their colleagues in 2010 with a molecule containing 356 atoms. The scientists estimate that atomic clusters containing half a million gold atoms could score a 23 on the macroscopic scale, a feat that would be challenging but not out of reach of future technology.

And what would Schrödinger's cat score on the new macroscopicity scale? The physicists calculated that a 4-kg cat, when in a quantum superposition where it sits in two positions spaced 10 cm apart for 1 second, would score a 57. Knowing this number won't make realizing it any easier, though. The physicists explain that this situation is equivalent to an electron existing in a superposition for 10⁵⁷ seconds, which is about 10³⁹ times the age of the universe.

© 2013 Phys.org