Game of go: A complex network

Could computers ever beat the best go players? Although unthinkable at this stage, this could soon become possible, thanks to CNRS theorists. For the first time, two scientists from the Theoretical Physics Laboratory and the Laboratory of Theoretical Physics and Statistical Models, have applied network theory to a game of strategy. Their findings, published in the journal Europhysics Letters, should help to improve future simulation programs.

The study of complex networks has attracted increasing interest over the past few years, fuelled in particular by the development of communication and information networks. This new research field is proving very useful for the description of complex systems such as social networks and the Internet. For instance, when network theory is applied to the Internet, every page is a node and hypertext links are links between the nodes. However, this type of approach had never been contemplated for the study of games of strategy such as go or chess. These games, which have a very long history and millions of players around the world, are extremely difficult to model. Computer programs have only been able to beat chess champions since the last fifteen years, and are still unable to compete with top go players. 

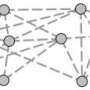
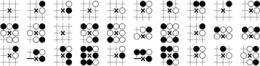
Using a database containing around 5 000 games played by professional and amateur go players in international tournaments, Bertrand Georgeot from the Theoretical Physics Laboratory and Olivier Giraud from the Laboratory of Theoretical Physics and Statistical Models applied network theory to this game of strategy. They constructed a network whose nodes are local patterns on the board, while the vertices (which represent the links) reflect the sequence of moves. This enabled them to recapture part of the local game strategy. In this game, where players place their stones at the intersections of a grid consisting of 19 vertical and 19 horizontal lines (making 361 intersections), the researchers studied local patterns of 9 intersections. They showed that the statistical frequency distribution of these patterns follows Zipf's law, similar to the frequency distribution of words in a language. 

Although the go network's features resemble those of other real networks (social networks or the Internet), it has its own specific properties. While the most recent simulation programs already include statistical data from real games, albeit at a still basic level, these new findings should allow better modeling of this kind of board game.