Secrets of the 'Levitating' Slinky: Viral web videos trigger physicists to explore a striking phenomenon

While holiday shoppers search frantically for the Moshi Monsters, LeapPad Explorers, or Lalaloopsy Silly Hair dolls atop their children's wish lists, many physicists remain engrossed in the properties of a simple 1940s-era toy -- the Slinky.

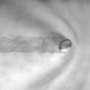
Spurred by a wave of recent Web videos showing the bottom of a dropped Slinky hovering dramatically in midair , physicists have provided new insights into this phenomenon, from the existence of shock waves in the falling Slinky, to a remarkably universal "levitation" time for a Slinky on other planets or moons despite their different gravitational fields.

In February 2000, the late science writer Martin Gardner posed a simple question intended for physics students, but also triggering a new round of papers and videos on the much-studied toy. Gardner wrote: "If you hold one end of a Slinky, letting it hang down and then drop it, what happens?"

"It turns out the bottom stays suspended, levitating in air for some period in time," said Shimon Kolkowitz, a physics graduate student at Harvard University in Cambridge, Mass. As an undergraduate at Stanford University in Palo Alto, Calif. in 2007, Kolkowitz wrote a paper now posted online for a class taught by his professor, physics Nobel Laureate Robert Laughlin.

And recently, Bill Unruh, a physics professor at the University of British Columbia, in Vancouver, heard some colleagues in the faculty lounge discussing a video of the levitating Slinky. As a result, Unruh, a world expert in black hole radiation, became captivated with Slinky physics.

Making calculations over a couple of days, Unruh wrote and posted a paper on the falling Slinky at the website arXiv.

Inspired by Gardner's riddle and earlier Slinky studies while putting together his paper, Kolkowitz calculated that the bottom of his metal Slinky would remain suspended for approximately three-tenths of a second. And only recently he made a surprising realization: the levitation time of the toy would be exactly the same if it were dropped on the moon, Jupiter or Mars, even with their vastly different gravitational fields.

Unruh found that the falling Slinky creates a shock wave through the toy, analogous to the blast wave of a bomb or a sonic boom created by aircraft. 

What in the world is going on?

"A Slinky is a simple spring, with the unique attribute that the spring in its natural resting state has all the coils touching one another," Unruh said.

"It's what's called a pretensioned spring," Kolkowitz added. "If you just leave it sitting on a desk on its side it'll actually be fully compressed."

Held from midair, the Slinky stretches out, quickly reaching a condition known as "equilibrium." in which the downward force of gravity is balanced by the upward tension of the coils above it.  When the top is released, the bottom stays suspended. The top of the Slinky collapses, so that the coils slam into each other. That collapse travels down as a wave through the Slinky. The bottom coils remain at rest until the top crashes into them.

And that's the key to understanding how the bottom of the Slinky remains suspended in midair for a short while.

"The bottom part of the Slinky hasn't deformed in any way," Kolkowitz explained. "Until that compression reaches the very bottom it won't move."

This levitation time -- approximately 0.3 seconds for Kolkowitz's own Slinky  -- would be the same on any planet or moon. Gravity and tension of the spring effectively cancel each other out.

Kolkowitz  said that one way of understanding this is that on the moon, the weaker gravitational field wouldn't stretch the Slinky as much, so the spring would compress more gently towards the bottom when dropped, taking the same 0.3 seconds to travel there. On Jupiter, the stronger gravitational field would stretch the suspended Slinky to a greater degree, so that the spring would have a larger distance to compress. But the more stretched-out top would snap back faster toward the bottom, resulting in the same levitation time.

As Kolkowitz pointed out, however, the Slinky's center of mass -- which shifts, but is always located somewhere in between the top and bottom of the toy -- still accelerates according to gravity all the way down to the ground from the moment it's released. So there's no violation of any of Newton's laws or Galileo's observations about falling objects.

The levitation time would only increase with a heavier Slinky and decrease if the coils were stiffer. The spring's mass and stiffness, Kolkowitz said, are the only two factors that affect the duration of levitation.

Kolkowitz pointed out this levitation effect would occur when any other spring or other elastic, nonrigid object is dropped -- and no object is completely rigid. "It's just that the Slinky is an especially easy system" in which to observe the effect, he said.

Another way to think about the levitation problem is that "the wave velocity in that Slinky is all that matters," Kolkowitz said. The wave velocity dictates "the length of time it takes information to reach the bottom of the Slinky," he said.  Once that wave slams into the bottom, the bottom no longer levitates.

In his analysis, Unruh observed that the collision of the upper part of the Slinky with the motionless lower coils is an example of a shock wave, analogous to a sonic boom that occurs in aircraft traveling faster than the speed of sound. Moreover, the wave that moves through the toy travels parallel to the compression of the Slinky, making it a "longitudinal" wave, the same type of wave as a sound wave. The normal speed of this wave in a Slinky is best measured by how many loops per second the wave passes through, about 50-100 loops per second for a typical Slinky, depending on such things as the thickness of the coils.

But in a falling Slinky, the coils crash into each other, creating a shock wave.

According to Unruh, the velocity of the shock wave, when it reaches the bottom, is notably higher than the normal velocity of the Slinky wave, breaking a sort of "sound barrier" in the Slinky.

"This behavior of shock waves is typical," he wrote in an email to Inside Science. "The blast wave of a bomb gets to you faster than the sound of a bomb would if it were very small."

A shock wave is simply a statement that something in a physical system changes abruptly, in this case, the velocity of the lower coils in the Slinky.

"There is a lot of interesting physics in a very, very simple system," said Unruh.

Kolkowitz said that this is an easy experiment for anyone to duplicate: use a stopwatch to time the fall when a friend drops a Slinky. This technique depends on the reflexes of the person running the stopwatch and therefore could introduce some error. 

Filming the falling Slinky with a video camera that captures a known number of frames per second and then counting the number of frames in which the bottom of the Slinky stays still would allow experimenters to more accurately calculate how long the Slinky's bottom stays suspended. 

"It's just such an easy experiment to do and it's kind of fun," Kolkowitz said.

Though Kolkowitz doesn't use Slinky experiments in his quantum physics work, he said the surprising insights on the levitating Slinky shows how studying and measuring even everyday objects can provide results that are "counterintuitive and not what you expect."