It takes three to tango: Nuclear analysis needs the three-body force

According to findings outlined by Dean and his colleagues in the May 20, 2011, edition of the journal Physical Review Letters, researchers who want to understand how and why a nucleus hangs together as it does and disintegrates when and how it does have a very tough job ahead of them.

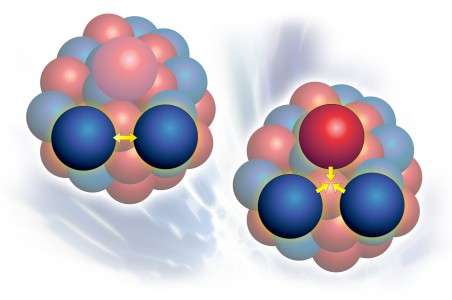
Specifically, they must take into account the complex nuclear interactions known as the three-body force.

Nuclear theory to this point has assumed that the two-body force is sufficient to explain the workings of a nucleus. In other words, the half-life or decay path of an unstable nucleus was to be understood through the combined interactions of pairs of protons and neutrons within.

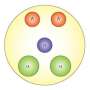
Dean's team, however, determined that the two-body force is not enough; researchers must also tackle the far more difficult challenge of calculating combinations of three particles at a time (three protons, three neutrons, or two of one and one of the other). This approach yields results that are both different from and more accurate than those of the two-body force.

Nuclei are held together by the strong force, one of four basic forces that govern the universe. (The other three are gravity, which holds planets, solar systems, and galaxies together and pins us to the ground, the electromagnetic force, which holds matter together and keeps us from, for instance, falling through the ground, and the weak force, which drives nuclear decay.)

The strong force acts primarily to combine elementary particles known as quarks into protons and neutrons through the exchange of force carriers known as gluons. Each proton or neutron has three quarks. The strong force also holds neighboring protons and neutrons together into a nucleus.

It does so imperfectly, however. Many nuclei are unstable and will eventually decay, emitting one or more particles and becoming a smaller nucleus. While we cannot say specifically when an individual nucleus will decay, we can determine the likelihood it will do so within a certain time. Thus an isotope's half-life is the time it takes half the nuclei in a sample to decay. Known half-lives range from an absurdly small fraction of a second for beryllium-8 to more than 2 trillion trillion years for tellurium-128.

One job of nuclear theory, then, is to determine why nuclei have different half-lives and predict what those half-lives are.

"For a long time, nuclear theory assumed that two-body forces were the most important and that higher-body forces were negligible," noted team member and ORNL computational physicist Hai Ah Nam. "You have to start with an assumption: How to capture the physics best with the least complexity?"

Two factors complicate the choice of approaches. First, two-body interactions do accurately describe some nuclei. Second, accurate calculations including three-body forces are very difficult and demand state-of-the-art supercomputers such as ORNL's Jaguar, the most powerful system in the United States. With the ability to churn through as many as 2.33 thousand trillion calculations each second, or 2.33 petaflops, Jaguar gave the team the computing muscle it needed to analyze the carbon-14 nucleus using the three-body force.

Carbon-14, with six protons and eight neutrons, is the isotope behind carbon dating, allowing researchers to determine the age of plant- or animal-based relics going back as far as 60,000 years. It was an ideal choice for this project because studies using only two-body forces dramatically underestimate the isotope's half-life, which is around 5,700 years.

"With Jaguar we are able to do ab initio calculations, using three-body forces, of the half-life for carbon-14," Nam said. "It's an observable that is sensitive to the three-body force. This is the first time that we've demonstrated at this large scale how the three-body force contributes."

The three-body force does not replace the two-body force in these calculations, she noted; rather, the two approaches are combined to present a more refined picture of the structure of the nucleus. In the carbon-14 calculation, the three-body force serves to correct a serious underestimation of the isotope's half-life produced by the two-body force alone.

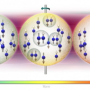
Dean and his colleagues used an application known as Many Fermion Dynamics, nuclear, or MFDn, which was created by team member James Vary of Iowa State University. With it, they tackled the carbon-14 nucleus using an approach known as the nuclear shell model and performing ab initio calculations—or calculations based on the fundamental forces between protons and neutrons.

Analogous to the atomic shell model that explains how many electrons can be found at any given orbit, the nuclear shell model describes the number of protons and neutrons that can be found at a given energy level. Generally speaking, the nucleons gather at the lowest available energy level until the addition of any more would violate the Pauli exclusion principle, which states that no two particles can be in the same quantum state. At that point, some nucleons bump up to the next higher energy level, and so on. The force between nucleons complicates this picture and creates an enormous computational problem to solve.

The carbon-14 calculation, for instance, involved a billion-by-billion matrix containing a quintillion values. Fortunately, most of those values are zero, leaving about 30 trillion nonzero values to then be multiplied by a billion vector values. As Nam noted, just keeping the problem straight is a phenomenally complex task, even before the calculation is performed; those 30 trillion matrix elements take up 240 terabytes of memory.

"Jaguar is the only system in the world with the capability to store that much information for a single calculation," Nam said. "This is a huge, memory-intensive calculation."

The job is even more daunting with larger nuclei, and researchers will have a long wait for supercomputers powerful enough to compute the nature of the largest nuclei using the three-body force. Even so, if the three-body force gives more accurate results than the two-body force, should researchers be looking at four, five, or more nucleons at a time?

"Higher-body forces are still under investigation, but it will require more computational resources than we currently have available," Nam said.

Provided by Oak Ridge National Laboratory